Реферат: Циклические коды. Коды БЧХ
Пример. Матрица G(n,k) для (7,4)-кода на основе порождающего многочлена g(x)=x3 +x+1, строится в следующей последовательности ![]()
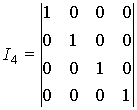 или
или ![]()
Определяется R4,3 , используя ![]() так
так ![]() как
как 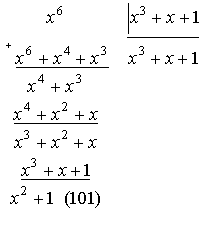
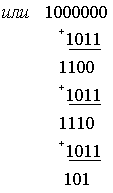
Аналогичным способом определяется 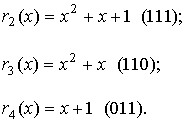
В результате получаем  или
или 
Используя выражение ![]() получим тот же результат.
получим тот же результат.
Строки матрицы G(n,k) можно определить непосредственно из выражения ![]() где
где ![]()
Проверочная матрица в систематическом виде строится на основе матрицы G(n,k) , а именно: ![]() где Ir - единичная матрица;
где Ir - единичная матрица; ![]() - матрица из G(n,k) в транспонированном виде.
- матрица из G(n,k) в транспонированном виде.
Пример. Для (7,4)-кода матрица H(n,k) будет иметь вид: 
Одна из основных задач, стоящих перед разработчиками устройств защиты от ошибок при передаче дискретных сообщений по каналам связи является выбор порождающего многочлена g(x) для построения циклического кода, обеспечивающего требуемое минимальное кодовое расстояние для гарантийного обнаружения и исправления t-кратных ошибок.
Существуют специальные таблицы по выбору g(x) в зависимости от предъявляемых требований к корректирующим возможностям кода. Однако у каждого циклического кода имеются свои особенности формирования g(x). Поэтому при изучении конкретных циклических кодов будут рассматриваться соответствующие способы построения g(x).
Коды БЧХ
Одним из классов циклических кодов, способных исправлять многократные ошибки, являются коды БЧХ.
Примитивным кодом БЧХ, исправляющим tu ошибок, называется код длиной n=qm -1 над GF(q), для которого элементы ![]() являются корнями порождающего многочлена.
являются корнями порождающего многочлена.
Здесь a - примитивный элемент GF(qm ).
Порождающий многочлен определяется из выражения ![]() где f1 (x),f2 (x)...- минимальные многочлены корней g(x).
где f1 (x),f2 (x)...- минимальные многочлены корней g(x).
Число проверочных элементов кода БЧХ удовлетворяет соотношению ![]()
Пример. Определить значение порождающего многочлена для построения примитивного кода БЧХ над GF(2) длины 31, исправляющего двух кратные ошибки (tu =2).
Исходя из определения кода БЧХ корнями многочлена g(x) являются: ![]() , где a - примитивный элемент GF(qm )=GF(25 ).
, где a - примитивный элемент GF(qm )=GF(25 ).
Порождающий многочлен определяется из выражения ![]() где f1 (x), f2 (x), f3 (x), f4 (x) - минимальные многочлены корней соответственно
где f1 (x), f2 (x), f3 (x), f4 (x) - минимальные многочлены корней соответственно ![]() .
.
Примечание.
Минимальный многочлен элемента b поля GF(qm ) определяется из выражения ![]() , где
, где ![]() - наименьшее целое число, при котором
- наименьшее целое число, при котором ![]() .
.
Значения минимальных многочленов будут следующими: 
Так как f1(x)= f2(x)= f4(x), то 
На практике при определении значений порождающего многочлена пользуются специальной таблицей минимальных многочленов (см. таблицу 8 приложения), и выражением для порождающего многочлена ![]() При этом работа осуществляется в следующей последовательности.
При этом работа осуществляется в следующей последовательности.
По заданной длине кода n и кратности исправляемых ошибок tu определяют:
- из выражения n=2m -1 значение параметра m, который является максимальной степенью сомножителей g(x); - из выражения j=2tu -1 максимальный порядок минимального многочлена, входящего в число сомножителей g(x).
- пользуясь таблицей минимальных многочленов, определяется выражение для g(x) в зависимости от m и j. Для этого из колонки, соответствующей параметру m, выбираются многочлены с порядками от 1 до j, которые в результате перемножения дают значение g(x).
В выражении для g(x) содержаться минимальные многочлены только для нечетных степеней a, так как обычно соответствующие им минимальные многочлены четных степеней a имеют аналогичные выражения.
Например, минимальные многочлены элементов ![]() соответствуют минимальному многочлену элемента a1 , минимальные многочлены элементов
соответствуют минимальному многочлену элемента a1 , минимальные многочлены элементов ![]() соответствуют минимальному многочлену a3 и т.п.
соответствуют минимальному многочлену a3 и т.п.
Пример. Определить значение порождающего многочлена для построения примитивного кода БЧХ над GF(2) длины 31, обеспечивающего tu =3.
Определяем значения m и j.