Реферат: Творческое мышление как результат принятия решения

А. Э. Симановский

1. Введение

Многие педагоги и психологи знают, что часто дети воспринимают сложные задания, как простые, а простые, как сложные. Аналогичная оценка, на наш взгляд, происходит, когда дети сталкиваются с творческой или алгоритмической задачей. Если ребенок решает, что перед ним алгоритмическая задача, то вариантов идей у него бывает очень мало, а то, что они предлагают в качестве решения – очень стереотипно и неоригинально. К примеру, при проведении эксперимента на изучение творческого мышления в классе я наблюдал мальчика, который в тесте “Круги” вместо того, чтобы на основе каждого круга рисовать новый и оригинальный рисунок, изображал рисунки, подсмотренные у своих товарищей спереди, сбоку, сзади … На мои попытки еще раз объяснить смысл творческой деятельности он возразил, что у других рисунки “верные”, а у него всегда получается неправильно. Таким образом, творческое задание не воспринимается им как творческое. Реже бывает, что дети воспринимают алгоритмическое задание, как творческое. В этом случае обычная “закрытая” задача понимается ими, как “открытая”. Нередко это ведет к ошибкам, так как учителя склонны оценивать лишь наличие или отсутствие навыков решения заданий данного типа, а не творческие “изыскания” детей. Лишь иногда подобное творчество приводит к верному решению и находит понимание и одобрение у учителей. Наиболее типичен случай маленького Гаусса, будущего знаменитого математика. Когда Гауссу было шесть лет, он учился в средней школе небольшого городка. Однажды учитель дал детям следующее задание по арифметике: “Кто из вас первым найдет сумму 1+2+3+4+5+6+7+8+9+10?” Все дети занялись вычислениями, а юный Гаусс поднял руку. “Вот!” – сказал он и назвал правильный ответ. “Каким образом, черт побери, тебе это так быстро удалось?” – воскликнул пораженный учитель. Гаусс объяснил, что если первое число прибавить к последнему, получается в сумме 11, если второе число прибавить к предпоследнему, тоже в сумме это составляет 11. И так далее! Всего таких пар – пять. 5 умноженное на 11 дает 55. Учитель похвалил мальчика и даже подарил учебник по математике. [1] На всех этих примерах видно, что субъект перед решением находится в позиции выбора – он должен определить характер и сложность стоящего перед ним задания. На одном полюсе стоят открытые задания, которые не имеют четко сформулированных условий, и большинство из них субъект должен определить самостоятельно. На другом полюсе стоят алгоритмические задачи с четким набором условий, определенным способом решения и единственным верным ответом. Можно предположить, что каждому типу задач соответствует определенная стратегия решения проблемной ситуации. Если субъект решает, что перед ним “открытое” задание, то он будет реализовывать “мягкую” стратегию анализа проблемной ситуации, а если решает, что задание, которое ему предстоит решать – “закрытое”, то стратегия решения в этом случае будет “жесткой”. Наше предположение основано на том, что субъект в той или иной степени владеет обеими стратегиями решения проблемных ситуаций.

2. Мягкая и жесткая стратегия решения проблемной ситуации

“Мягкой” стратегия была названа из-за того, что она предполагает исследование большого количества сведений и обращение внимания на события малой вероятности. При этом субъект старается выявить скрытые, “латентные” свойства изучаемой ситуации. Напротив, при “жесткой” стратегии субъект ограничивает себя, ориентируясь на самое важное в ситуации, выделяя события высокой вероятности.

Данное положение можно проиллюстрировать на модели четырехклеточной прямоугольной матрицы. По горизонтали мы обозначим два полярных стиля решения задач, а по вертикали характер предлагаемых заданий. (см. Рис.1)

Рис.1

Достоинства “мягкой” стратегии, таким образом, наиболее проявляется в “открытых” заданиях, в “закрытых” же заданиях она может приводить к перерасходу времени и поиску таких решения, которые в данных обстоятельствах не нужны Однако в некоторых случаях (таких, как с Гауссом) “мягкая” стратегия также может приводить к быстрому результату, помогая обнаружить другой способ решения. Достоинства “жесткой” стратегии наиболее проявляются в закрытых заданиях, требующих быстрого и однозначного ответа. В заданиях “открытого типа” “жесткая” стратегия приводит к неоправданному самоограничению и неоригинальности предлагаемых решений.

Естественно, что каждая из названных стратегий оптимальна для своего типа задач, но скорее всего, их выбор осуществляется не только на основе объективного анализа типа предстоящего задания.

Можно также предположить, что существуют внешние и внутренние факторы, влияющие на процесс выбора стратегий. Среди внешних факторов наиболее важным представляется лимит времени, отводимый на выполнение задания, мера ответственности, возлагаемая на субъекты и характер подкреплений.

“Жесткая” стратегия является более определенной и проверенной. Поэтому она скорее всего будет чаще выбираться людьми при временном дефиците и повышенной мере ответственности за решение. Это можно объяснить законом Иеркса-Додсона, который, как известно, гласит, что при повышенной мотивации люди склонны выбирать более простые варианты заданий.

“Мягкая” стратегия предполагает переработку бóльшего объема информации, чем “жесткая”, поэтому она естественно может восприниматься как более сложная и трудоемкая. Однако случай с Гауссом свидетельствует, что не всегда временной дефицит способствует выбору “жесткой” стратегии. Здесь мог сказаться либо характер подкреплений, идущий со стороны взрослого, либо внутренние (личностные) детерминанты выбора.

3. Влияние подкреплений на характер выбора стратегии решения задач

Рассмотрим характер возможных подкреплений при выборе стратегии мышления. Это удобно сделать в форме платежной матрицы.

Содержание оцениваемых параметров матрицы может быть различным, но мы выбрали те их них, которые: во-первых, могут повлиять на выбор той или иной стратегии, во-вторых, те, которыми можно легко манипулировать, и в-третьих, те, которые достаточно очевидны и понятны для испытуемых. Так, к примеру, мы отбросили такой параметр, как оригинальность, так как его достаточно сложно интерпретировать и ранжировать по степени выраженности (см. В.Н.Дружинин. 1999. с.199-208).

Всем трем выделенным нами критериям в наибольшей степени подходят два параметра: время, отводимое на решение задания и количество предлагаемых решений. Так, к примеру, на Рис.2 показана платежная матрица, где мы можем по-разному подкреплять большое и малое количество решений, высокую и низкую скорость действия субъекта.

Рис.2

Когда мы поощряем творческий подход к заданию, не реагируя на время, испытуемый получает за два и большее количество решений по 5 баллов, а за одно только 1 балл.

На Рис.3 показана платежная матрица, когда мы, поощряя творческий подход к задаче, ограничиваем время решения.

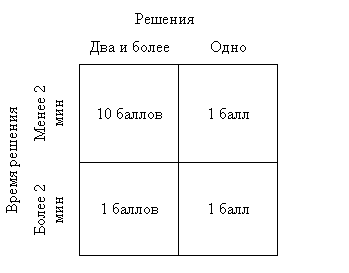
Рис.3

На Рис 4. показана платежная матрица, где поощряется жесткий подход к решению задачи.

Примечание: Каждый положительный вариант решения поощряется, тогда как отсутствие решения может оцениваться как нулем, так и баллами с отрицательными значениями.

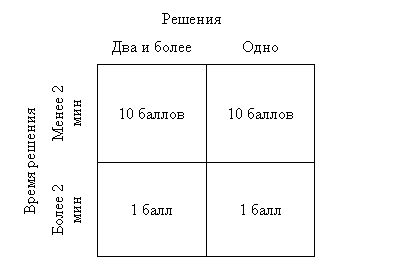
Рис. 4

Данные платежные матрицы предполагается использовать в эксперименте с модифицированным тестом Лачинса “Решение арифметических задач”. Модификация данного теста представляла собой упрощение арифметических заданий и сокращение их количества до восьми. В каждой задаче дается три пустых сосуда различной емкости. На сосудах нет никаких отметок или делений, известна только их емкость. С помощью сосудов необходимо отмерить или получить путем определенного манипулирования ровно столько жидкости, сколько требуется по условиям каждой задачи. Манипулирование производится в уме, а способ решения записывается. Обычно на одну задачу дается не более 2 минут – этим определяется показатель платежной матрицы. Особенностью этих задач является то, что некоторые из них имеют только один вариант решения, а некоторые – два и более. Таким образом, по количеству даваемых ответов в заданиях мы можем проверить, какая стратегия реализовывалась испытуемыми – “жесткая” или “мягкая” в случаях с разным характером подкрепления.

4. Влияние личностных особенностей на выбор стратегии решения задач

Сравнивая открытые и закрытые задания можно обнаружить, что они различаются не только по количеству анализируемых факторов, количеству гипотез, но и по критериям предлагаемого решения. В закрытых задачах критерии решения определены условиями и задаются до предъявления задачи испытуемому. В открытых заданиях критерий решения испытуемый для себя определяет сам. Именно в таких случаях актуальна поговорка “Лучшее враг хорошего”. Субъект должен для себя решить, когда закончить анализ ситуации. Этот момент в основном зависит от уровня притязаний субъекта (Г.Саймон; Ю.Козелецкий).

На наш взгляд, степень “мягкости” стратегии решения задачи прямо коррелирует с уровнем притязаний личности. Высокий уровень притязаний таким образом провоцирует выбор мягкой стратегии, а низкий уровень – “жесткой”. Уровень притязаний при этом понимается как прогнозируемая субъектом степень успешности в данном виде деятельности. Ю.Козелецкий определяет уровень притязаний, как (точку) выделение значения на объективной шкале достижений… (с.293). В случаях, когда шкала достижений может быть выражена одним параметром, уровень притязаний называют одномерным; в случае, когда шкала достижений выражена несколькими параметрами, а уровень притязаний является вектором параметров, он называется многомерным.

Для нас показатель уровня притязаний особенно важен, так как он показывает взаимосвязь мотивации достижения с творческим мышлением субъекта. Развивая мотивацию достижения и тем самым повышая уровень притязаний мы таким образом усиливаем тенденцию к выбору “мягкой”, творческой стратегии решения задач. В свою очередь, развитость мотивации достижения мы рассматриваем как главный показатель личностного благополучия ребенка в современной школе (см. Вестник ИПК, 1999г.).

Данная концепция показывает, что непроявление творческого мышления в школе не всегда есть результат его несформированности и отсутствия у ребенка, а является следствием определенного педагогического и психологического воздействия, детерминирующего “жесткую” стратегию решения проблемных ситуаций.

Список литературы

--> ЧИТАТЬ ПОЛНОСТЬЮ <--