Реферат: Установка для определения релаксационных характеристик низкомодульных полимерных материалов

Отличительной особенностью низкомодульных полимеров (НП), в частности резин, является сильная зависимость напряжения и деформации от времени действия силы и скорости нагружения. Данная зависимость является важнейшей характеристикой вязкоупругих материалов, получившая название релаксации. Релаксационные процессы протекающие в НП, зависят от соотношения энергии взаимодействия между структурными элементами полимера и энергии теплового движения этих элементов, и характеризуют вязкоэластические свойства материала. Изменение температуры приводит к соответствующему изменению энергии теплового движения, что обуславливает зависимость механических свойств НП от температуры.

В физике полимеров [1] в качестве основных релаксационных процессов обычно рассматриваются a-процесс релаксации, соответствующий переходному состоянию (область II), связанный с подвижностью свободных сегментов молекул, и l-процесс (область III), зависящий от подвижности сетки, образованной микроблоками надмолекулярной структуры полимеров. Время релаксации a-процесса составляет доли секунды, а более медленного l-процесса – от 101 до 108с. Кроме этих релаксационных процессов, существуют более быстрые и более медленные, однако с основном НП работают именно в этой временной области воздействия.

Практически с самого момента появления лазеров они оказались в центре внимания аналитиков как источник высокоэнергетического излучения, при взаимодействии которого с веществом возможно локальное испарение пробы и образование светящейся плазмы. Лазерное излучение можно сфокусировать в любой точке жидкой, газообразной или твердой пробы. В последнем случае это позволяет проводить не только интегральный анализ, но и получать информацию о пространственном распределении химических элементов в пробе. Однако, несмотря на широко ведущиеся разработки лазерных методов анализа, существует значительный разрыв между потребностями в таких методах и существующими реализациями для повседневной практики. Одним из факторов, существенно сдерживающих широкое применение метода, является труднодоступность, а часто и просто отсутствие, твердых образцов сравнения. Состав пара и ионной компоненты плазмы может существенно отличаться от элементного состава образца из-за неодинаковой степени поступления их с поверхности. Эти различия могут возникать на стадиях плавления, кипения, образования капель, диффузии в жидкой фазе и т.д. Использование сдвоенных лазерных импульсов излучения для анализа свежих растительных и биологических объектов приводит к дополнительным возможностям прикладного использования энергии лазерного излучения. Одной из таких потенциальных возможностей является возможность минерализации пробы первым импульсом, а затем вторым импульсом проведение непосредственно атомно-эмиссионного спектрального анализа. Изучение особенностей поступления химических элементов с поверхности и объема пористых тел может послужить основой для разработки образцов сравнения для анализа указанных объектов, так как большая часть биологических объектов представляют собой пористые тела. Многие вопросы, возникающие при создании оптимальных условий для проведения исследований процессов выхода элементов и одновременного экспресс-анализа удаляемых и остающихся элементов с поверхности могут быть эффективно решены при использовании лазерного многоканального атомно-эмиссионного спектрометра LSS-1 (производство СП «ЛОТИС ТИИ», Беларусь, г. Минск). Спектрометр включает в себя в качестве источника возбуждения плазмы двухимпульсный неодимовый лазер с регулируемыми энергией и интервалом между импульсами (модель LS2131 DM). Лазер обладает широкими возможностями как для регулировки энергии импульсов (до 80 мДж), так и временного сдвига между сдвоенными импульсами (0-100 мкс) излучения. Лазер может работать с частотой повторения импуль- сов до 10 Гц и максимальной энергией излучения каждого из сдвоенных импульсов до 80 мДж на длине волны 1064 нм. Длительность импульсов » 15 нс. Временной сдвиг между сдвоенными импульсами может изменяться с шагом 1 мкс. Лазерное излучение фокусировалось на образец с помощью ахроматического конденсора с фокусным расстоянием 100 мм. Размер пятна фокусировки примерно 50 мкм. Все эксперименты проводились в атмосфере воздуха при нормальном атмосферном давлении. Свечение плазмы собиралось с помощью аналогичного конденсора на передние поверхности двух кварцевых волокон диаметром 200 мкм и направлялось на входные щели двух спектрометров типа SDH-1. Регистрация спектра проводилась с помощью ПЗС- линеек TCD 1304 AP (3648 пикселей). Запуск системы регистрация спектра осуществлялась синхронно с приходом второго импульса. Как видно из приведенных возможностей спектрометра управлять параметрами плазмохимического процесса и эрозией поверхности пористых тел можно, изменяя как плотность падающей энергии лазерного излучения, так и время задержки прихода второго сдвоенного лазерного импульса. В качестве модельных систем нами выбраны беззольные фильтры, как наиболее близко подходящие по своей структуре и поглощательной способности для водных растворов солей различных элементов. При проведении экспериментов фильтр наклеивался на поверхность держателя образцов, а затем на поверхность фильтра наносились растворы солей исследуемых элементов. Установлено, что процессы взаимодействия излучения с поверхностью образцов существенно зависят от метода изменения падающей плотности мощности одиночного импульса. Так при изменении плотности мощности падающего излучения (l=1,064 нм, длительность одиночного импульса 15 нс) изменением энергии накачки (энергия накачки 10-15 Дж, энергия излучения 20-80 мДж) скорость испарения легкоплавких элементов натрия и лития постепенно возрастает, а затем падает. При изменении пятна фокусировки (изменение плотности мощности) наблюдается определенная периодичность, зависящая от энергии падающего излучения и расстояния за точкой точной фокусировки. При использовании режима сдвоенных лазерных импульсов (временная задержка между импульсами от 0 до 100 мкс) результирующая картина плазмообразования и формирования поверхности еще более усложняется. Полученные результаты можно объяснить на качественном уровне следующим образом. Вблизи поверхности образцов, содержащих в качестве компонентов легкоплавкие металлы Na, Li, имеющие относительно низкие температуры кипения пробой эрозионного факела металлических атомарных паров происходит при небольшом превышении интенсивности лазерного излучения значением, необходимым для образования факела. В первом эксперименте при изменении пятна площади фокусировки количество микродефектов изменяется. При начальном пятне размером примерно 50 мкм количество таких микродефектов невелико. При увеличении пятна фокусировки в область облучения попадает все увеличивающее число микродефектов и порог пробоя воздуха у поверхности образца значительно понижается. При использовании режима сдвоенных импульсов на первичные процессы плазмообразования будут накладываться процессы нагрева и испарения аэрозолей, образовавшихся при первом импульсе, вторым импульсом излучения. Общая черта всех моделей, описывающих пробой в аэродисперсных средах – это нагрев и испарение аэрозольных частиц. Большинство из них рассматривают аэрозольные частицы как фактор, облегчающий пробой за счет развития электронной лавины в продуктах разрушения частиц.Дополнительными, а может быть и основными в нашем случае, механизмами повышения концентрации Na в плазме и соответственно уменьшением в поверхности могут быть ударные и тепловые волны, связанные с формированием пробоя в атмосфере, которые будут воздействовать на поверхность образца в некотором месте, что приводит к дополнительному нагреванию точки поверхности при сжатии. Даже при небольшом увеличении температуры (на 50-100 0С) натрий и литий легко испаряются с поверхности с несколько большей глубины, чем при воздействии только света. Подтверждением этого механизма увеличения количества атомов натрия и лития в плазме может служить тот факт, что если после действия мощного сдвоенного импульса излучения зарегистрировать спектр плазмы с облученного места, то интенсивность линий натрия и лития значительно уменьшается (от начальной концентрации 10-4 % до 10-7 %).Исследование процессов эрозии и модификации поверхности пористых тел показало, что обеднение поверхности натрием и литием весьма существенно. Природа подобных процессов связана как с отличием физических свойств элементов, входящих в сложный по микроструктуре и составу образец, так взаимным воздействием сдвоенных лазерных импульсов на поверхность

Наиболее полную информацию о релаксационных свойствах резин дает временная зависимость модуля упругости E(t), типичный вид которой представлен на рис. 1 [1]. Как видно из рисунка, имеются три области, описывающие деформационные свойства резины с характерными значениями модулей упругости: I – область стеклообразного состояния с модулем Ес, II – переходная область с модулем, меняющемся от Ес до начального значения высокоэластичного (равновесного) модуля и III – область высокоэластичности, в которой происходит медленная физическая релаксация, по завершению которой материал характеризуется значением равновесного модуля упругости Ер. [1]. При этом ход кривой Е = f(lgt) для различных полимеров, в зависимости от химической природы и технологических особенностей изготовления будет различным и обусловлен характерными релаксационными процессами, происходящими в материале.

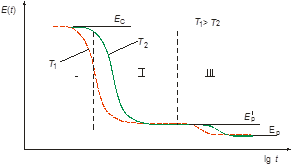
Рис. 1. Временная зависимость модуля упругости E(t).

Согласно теории температурно-временной эквивалентности, нагревание полимерных материалов приводит к параллельному смещению кривой Е=f(lgt) в область меньших значений времени [2]. При этом в большей степени проявляются более медленные процессы релаксации (рис. 1). Совершенно очевидно, что варьируя временем воздействия и температурой, можно получать релаксационные кривые модуля упругости в широком диапазоне. Такой подход даёт ценную информацию о вязкоэластических свойствах НП.

Для этих целей предлагается использовать метод динамического индентирования, который разработан в ИПФ НАН Беларуси и реализован в приборе ИМПУЛЬС 1Р [3] (рис. 2). Данный метод заключается в нанесении удара жестким индентором (бойком) по испытуемому материалу и непрерывной регистрации процесса контактного взаимодействия индентора с материалом. Исходной информацией о свойствах материала является массив текущей скорости перемещения индентора V(t) в контакте с материалом. Дифференцирование скорости с последующим умножением на массу индентора позволяет получить текущее значение контактного усилия P(t), а интегрирование – значение перемещения α(t). Наиболее интересной для анализа является зависимость контактное усилие-глубина внедрения индентора, которую можно получить, исключив время как параметр из соответствующих кривых. Данная зависимость состоит из двух характерных этапов: первый этап (активная часть удара) – этап нагружения материала, при котором индентор внедряется в материал и достигает своего максимального перемещения αмакс, и второй (пассивная часть удара) – этап разгрузки, на котором происходит отскок индентора и восстановление отпечатка.

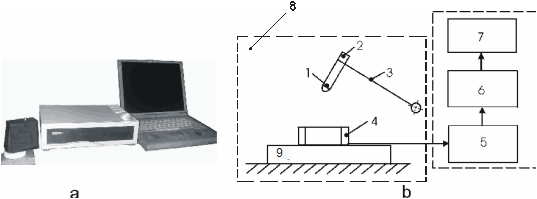
Рис. 2. а – общий вид прибора ИМПУЛЬС 1Р. b- блок-схема установки: 1- индентор, 2- магнит, 3- поворотный рычаг, 4- индукционный датчик, 5 –предварительный усилитель, 6 – аналого-цифровой преобразователь, 7 –персональный компьютер, 8 – термокамера; 9 – испытуемый образец.

Прибор ИМПУЛЬС-1Р позволяет определять релаксационный динамический модуль упругости Eр на любом этапе удара, а также ряд других параметров материала, характеризующих релаксационные свойства: вязкость h, эластичность, тангенс угла механических потерь tg δ [3]. При импульсном нагружении материал проявляет вязкие свойства, которые невозможно оценить при статическом воздействии, кроме того, динамическое нагружение моделирует наиболее жесткие условия, которым может подвергаться материал во время эксплуатации [4].

Диоксид кремния SiO2 может существовать во множестве различных кристаллических форм (α- и β-кварц, α- и β-кристобалит и др). Большинство из этих структур образовано из тетраэдров с атомом кремния в центре и атомом кислорода в углах. Эти структуры слабо различимы по энергии и отличаются друг от друга главным образом способом соединения тетраэдров. Хотя строение большинства разновидностей диоксида кремния хорошо изучено, структура β-кристобалита до сих пор не ясна (существует, по меньшей мере, пять вариантов). Структуру β-кристобалита часто называют «идеальным» β-кристобалитом так как она имеет высокую симметрию. Элементарная ячейка β-кристобалита содержит две формульные единицы SiO2. Реальная структура β-кристобалита может быть представлена как результат разворота на ±20º каждого тетраэдра SiO4 из идеальной структуры вокруг оси четвертого порядка. Это приводит к изменению кубической симметрии в тетрагональную с пространственной группой и двумя формульными единицами SiO2 в элементарной ячейке [1,2]. Характеристическими параметрами кристаллической структуры подобной халькопириту являются параметры решетки (а и с), тетрагональное сжатие (γ=с/а=1.577), смещение анионов из узлов ГЦК подрешетки (х=0.1234, в единицах a), угол разворота тетраэдров φ=20º и валентный угол θ(O-Si-O)=147.6º.

Соединения LiBO2 [3], NaPN2 и LiPN2 [4] со структурой халькопирита имеют изоэлектронное сходство с семейством халькопирита (16 электронов в элементарной ячейке) и одновременно являются кристаллохимическими аналогами β-кристобалита. Основными особенностями этой группы кристаллов являются: сильное тетрагональное сжатие 1.403, 1.55 и 1.56; большое смещение анионов 0.1239, 0.1574 и 0.1669, в единицах a; угол разворота тетраэдров φ 26.4º, 32º и 34.2º, валентные углы 137.4º, 128.7º и 125.4º; для NaPN2, LiBO2 и LiPN2, соответственно.

Целью настоящей работы является расчет из первых принципов в рамках функционала локальной электронной плотности электронной структуры соединений SiO2, NaPN2, LiBO2 и LiPN2 с решеткой халькопирита. В расчетный базис включались псевдоатомные sp3d5-орбитали каждого атома. Сходимость по полной энергии обеспечивалась не хуже 0.001 а.е. Вычисление зонной структуры всех соединений проводилось в точках высокой симметрии Т(0,0,1), Г(0,0,0), N(0.5,0.5,0), P(0.5, 0.5, 0.5) в единицах () и вдоль линий их соединяющих. Были вычислены также плотность состояний N(E) и распределение заряда валентных электронов ρ(r).

Результаты вычислений зонной структуры и плотности состояний ряда соединений SiO2, NaPN2, LiBO2 и LiPN2 представлены на рис.1. За начало отсчета шкалы энергий выбрано положение последней заполненной валентной зоны. Валентная зона SiO2 состоит из четырех разрешенных энергетических полос, что не характерно для соединений со структурой халькопирита, валентная зона которых имеет три разрешенных полосы энергий. Вторая связка валентных зон включает четыре ветви, а не две, как в халькопиритах. Вершина валентной зоны SiO2 реализуется в точке Т и следовательно кристалл является непрямозонным.

Структура валентной зоны LiBO2 во многом подобна структуре валентной зоны SiO2. Основное отличие этих соединений сосредоточено в строении вершины валентной зоны, где абсолютный максимум располагается в точке Г, а в точках T и N имеются локальные максимумы. По этой причине LiBO2 следует отнести к прямозонным соединениям.

Пниктиды LiPN2 и NaPN2 по строению валентной зоны очень похожи между собой и имеют определенное сходство с кристаллами SiO2 и LiBO2. Оба соединения LiPN2 и NaPN2 являются непрямозонными с вершиной валентной зоны в точке Т. Смещение абсолютного максимума валентной зоны в кристаллах со структурой халькопирита из точки Г в точку Т является следствием сильного тетрагонального сжатия в них. Интегральная трансформация энергетического спектра при переходе от структуры кристобалита к структуре халькопирита прослеживается на графиках плотности состояний, который условно разбит на три структуры А, В и С. Каждая из этих структур имеет подструктуры с соответствующей нумерацией.

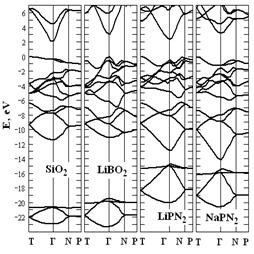
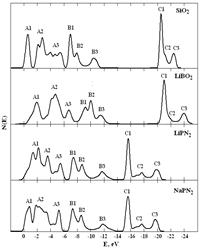
Рис.3. Зонная структура и плотность состояний кристаллов SiO2, LiBO2, LiPN2 и NaPN2

Анализ вкладов атомных орбиталей в кристаллические орбитали показал, что нижняя связка валентных зон соединений SiO2, LiBO2, LiPN2 и NaPN2 состоит в основном из s-состояний анионов.

Следующая связка зон из четырех ветвей для SiO2 имеет преобладающий вклад s-состояний кремния в нижнюю ветвь (76%) и почти равный вклад (46-47%) p-состояний кремния и кислорода в оставшиеся три ветви. Для соединений LiBO2, LiPN2 и NaPN2 эта связка зон содержит преимущественный вклад s-состояний «тяжелого» катиона (B, P).

Рассмотрены особенности кристаллической структуры и магнитного упорядочения нового поколения магнитных полупроводниковых гомогенных оксидных материалов, которые могут быть использованы для создания устройств спиновой электроники. До последнего времени технологический прогресс в этой области сдерживался отсутствием материалов с температурой Кюри выше 300 K. Поиск полупроводниковых материалов, обладающих ферромагнитным упорядочением при комнатных температурах, ведется в разных направлениях, но самой рациональной является методология DMS (diluted magnetic semiconductor), так как растворение магнитных примесей в полупроводниковой матрице позволяет в сжатые сроки «запустить» создание спинтронных устройств, заменив в существующих электронных схемах полупроводниковые рабочие элементы на спин-полупроводниковые.

В настоящей работе представлены результаты исследования модельных материалов на основе ограниченных твердых растворов антиферромагнитных оксидов кобальта в диамагнитном оксиде цинка – полупроводника-пьезоэлектрика. Прежде всего, методами физико-химического анализа исследованы фазовые равновесия и построена концентрационная диаграмма системы Zn – Co – O [1]. По данным РФА, растворимость оксидов кобальта в вюртцитной матрице ZnO достигает 20 мол. %, при этом граничные составы твердого раствора изменяются с температурой. Заметная растворимость оксидов кобальта в ZnO наблюдается выше температуры 1173 K, при которой удается получить гомогенные образцы номинального состава Zn0.95Co0.05O, при 1273 K - Zn0.9Co0.1O, а при 1373 K - Zn0.8Co0.2O. Дальнейшее увеличение температуры приводит не к увеличению растворимости, а к распаду твердого раствора. Показано, что кристаллические растворы на основе ZnO, CoO и Co3O4 в зависимости от условий синтеза и отжига, обладают различной кислородной нестехиометрией при фиксированном отношении Zn/Co. Однако управление свойствами Zn1-XCoXO1+d с помощью задаваемого d в настоящее время не решаемая задача.

Был выбран другой возможный фактор влияния - введение еще одного магнитного иона в вюртцитную структуру Zn1-XCoXO1+d.. Поскольку Fe и Ni даже на 1 % не замещают позиции Zn2+ этом твердом растворе, т.е., согласно нашим данным, не образуют гомогенные поликристаллы номинального состава Zn0.89Co0.10Fe(Ni)0.01O, то для системного исследования были выбраны оксиды лантаноидов. Установлено, что оксиды четырех лантаноидов (Pr, Nd, Sm и Eu) способны образовывать с Zn0.9Co0.1O1+d ограниченные твердые растворы. В случае европия, растворимость достигает состава Zn0.87Co0.10Eu0.03O1+d.

Методом измерения пондеромоторной силы в магнитном поле 0,86Т и интервале температур 77 - 700К изучены зависимости удельной намагниченности s=f(T) и магнитной восприимчивости 1/χ=f(T) полученных материалов. Оказалось, что кривые удельной намагниченности исследованных образцов, как системы Zn–Co–O, так и систем Zn – Me –Co–O (где Me=Pr, Nd, Sm, Eu) практически одинаковы. Между ними наблюдается лишь небольшое различие в абсолютных значениях намагниченности. Кривые удельной намагниченности и магнитной восприимчивости указывают на наличие двух критических температур Т1≈ 125К и Т2≈ 650К. Можно предположить, что при температуре Т1 наблюдается фазовый переход «магнитный порядок I – магнитный порядок II», а при температуре Т2 –переход «магнитный порядок II – магнитный беспорядок». Анализ температурных зависимостей s=f(T) и 1/χ=f(T) показывает, что при температуре Т2 происходит переход в парамагнитное состояние. Значения удельной намагниченности всех образцов при температуре жидкого азота s < 0,5 Гс∙см3/г., поэтому проблематично говорить только о ферромагнитном упорядочении, несмотря на то, что при повышении температуры величина удельной намагниченности плавно уменьшается. В диапазонах температур 150-500 К и 650-725 К поведение магнитной восприимчивости подчиняется закону Кюри-Вейсса:

,

где Cx - постоянная Кюри-Вейсса, а Qx – парамагнитная температура.

Определенные из экспериментальных зависимостей 1/χ = f(T) парамагнитные температуры имеют отрицательные величины, что однозначно определяет знак интеграла обменного взаимодействия J1,

,

--> ЧИТАТЬ ПОЛНОСТЬЮ <--