Реферат: Устойчивость линейной системы авторегулирования

Задача оптимального синтеза линейной системы авторегулирования при случайных воздействиях заключается в определении такой структуры и параметров системы, при которых ошибки минимальны. Это так называемая задача оптимальной линейной фильтрации. Она была решена Колмогоровым, Винером, Калманом. В постановке Винера и Колмогорова входные процессы задаются их энергетическими спектрами. Для САР входными процессами являются задающее x _з (t ) и возмущающее x _в (t ) воздействия с энергетическими спектрами S_{x з} (w) и S_{x в} (w). Оптимальная частотная характеристика без учета физической реализуемости системы имеет вид:

К _опт (j w ) = S_{x з} (w)/[S_{x з} (w) + S_{x в} (w)].

Объясняется такая форма частотной характеристики просто. В области частот, где S_{x в} (w) = 0 АЧХ замкнутой системы равна 1, что и требуется для безошибочного слежения. В области частот, занятых спектром возмущающего воздействия, коэффициент передачи должен быть тем меньше, чем больше интенсивность помехи.

Неудобство данного подхода для синтеза САР заключается в том, что определяется только частотная характеристика замкнутой системы, а структура системы неочевидна. В этом отношении удобнее подход Калмана, определяющий структуру оптимальной системы. В отличие от предыдущего подхода, описывающего задающее воздействие энергетическим спектром, в подходе Калмана задающее воздействие образуется пропусканием белого шума через формирующий фильтр, который строится как устройство с обратной связью. Формирующий фильтр описывается векторным дифференциальным уравнением, которое называется уравнением состояния:

d X _з ( t )/dt = AX _з ( t ) + Bn (t ),

где n (t ) – белый шум,

X _з ( t ) – вектор-столбец переменных состояния, которыми обычно являются сам процесс x _з (t ) и его производные,

А – матрица системы,

В – матрица управления.

Для формирования задающего воздействия к уравнению состояния добавляется уравнение наблюдения:

x _з (t ) = CX _з (t ),

где С – матрица наблюдения, устанавливающая связь процесса x _з (t ) с вектором переменных состояния X _з (t ).

x з (t ) X з (t ) n (t ) А С 1/р В

Рис. 9

По этим уравнениям построена модель, представленная на рис. 9. Сформированное таким образом задающее воздействие поступает на вход САР вместе с возмущающим воздействием, которое считается белым шумом. Доказано, что оптимальный фильтр Калмана повторяет структуру формирующего фильтра с точностью до матричного коэффициента передачи К (рис. 10).Элементы матрицы К и определяют оптимальность системы.

y (t )=x з (t ) С А 1/р K x в (t ) x з (t )

Рис. 10

Проиллюстрируем сказанное на примере системы первого порядка. Пусть в качестве формирующего фильтра используется интегрирующая цепь с постоянной времени Т _ф . Ее передаточная функция: К _ф (р ) = 1/(1 + рТ _ф ). Этой передаточной функции соответствует дифференциальное уравнение в операторной форме:

(рТ _ф + 1)x _p (t ) = n (t ).

В обычной форме оно записывается так:

.

Отсюда

.

Модель, построенная по этому уравнению, изображена на рис. 31

n (t ) 1/T ф 1/T ф 1/p x з (t )

Рис. 11

Оптимальная система представлена на рис. 12.

Оптимальное значение коэффициента передачи:

, (13)

где r - отношение спектральных плотностей случайных процессовn (t ) и x _в (t ).

1/T ф y (t )=x (t ) 1/p K x в (t ) x з (t )

Рис. 12

Дисперсия ошибки слежения в оптимальной системе:

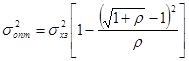.(14)