Реферат: Устойчивость линейной системы авторегулирования

Отличие коэффициента передачи К от оптимального приведет к увеличению ошибки. Ошибка складывается из динамической ошибки и ошибки по возмущению. Дисперсия динамической ошибки

.

Спектральная плотность задающего воздействия

.

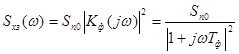Дисперсия задающего воздействия

.

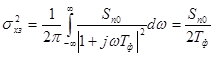Выразим спектральную плотность S_{n 0} процесса n (t ) через дисперсию задающего воздействия: S_{n 0} = 2T _ф s² _{x з} .

Частотная характеристика разомкнутой системы для схемы, изображенной на рис. 32, имеет вид:

.

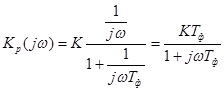И соответственно,

.

Тогда

. (15)

К T ф =1 К T ф =5 К T ф =20 S (w) 0,5 0,75 0,25 10 w,рад/с 0,1 1 S К

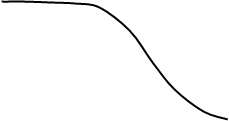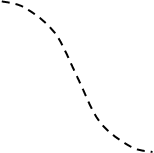Рис. 13

Для пояснения причины уменьшения динамической ошибки с ростом коэффициента передачи К обратимся к рис. 13, на котором представлены энергетический спектр процесса x _з (t ) (пунктирная линия) и АЧХ замкнутой системы при различных значениях КТ _ф (сплошные линии). Видим, что чем больше КТ _ф , тем меньше отличие коэффициента передачи замкнутой системы от 1 в области частот, занятых спектром задающего воздействия.

Дисперсия ошибки по возмущению вычисляется по формуле:

.

Так как спектральная плотность возмущающего воздействия в r раз меньше спектральной плотности S_{n 0} , то

и

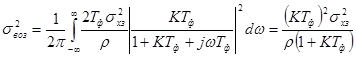. (16)

Дисперсия ошибки по возмущению увеличивается с ростом КТ _ф , так как увеличивается площадь под АЧХ замкнутой системы. Зависимость дисперсии суммарной ошибки s² = s² _дин + s² _воз от КТ _ф показана на рис. 14 для различных значений r. Минимум достигается при оптимальном значении коэффициента передачи. Следует отметить, что оптимум не очень критичен и при двукратном отличии коэффициента передачи от оптимального дисперсия ошибки увеличивается на 15 – 20 %.

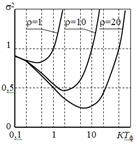
Рис.

Рассмотрим теперь, к какому увеличению дисперсии приведет отличие структуры системы от оптимальной. Допустим, что система первого порядка (рис. 32) осуществляет слежение за процессом x _з (t ), образованным из белого шума формирующим фильтром второго порядка с пере-даточной функцией К _ф (р ) = =1/(1 + рТ _ф1 )² . Подберем Т _ф1 так, чтобы площади под |К _ф (j w)½² для однозвенного и двухзвенного фильтров были одинаковыми. Тогда будет соблюдаться равенство дисперсий выходных процессов обоих фильтров при одинаковой спектральной плотности входного белого шума. Это условие выполняется при Т _ф1 = Т _ф /2. На рис. 15 представлены АЧХ фильтров: однозвенного (сплошная линия) и двухзвенного (пунктирная линия). Из-за отличия спектров задающего воздействия изменится динамическая ошибка. Дисперсия динамической ошибки станет равной:

.

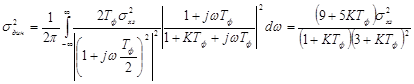Дисперсия ошибки по возмущению останется прежней, так как частотная характеристика замкнутой системы не изменилась. На рис. 36 показано, во сколько раз увеличивается минимальная дисперсия суммарной ошибки в системе с неоптимальной структурой по сравнению с дисперсией ошибки в оптимальной системе в зависимости от r.

0 0,25 0,75 0,5 S 1 0,1 wT ф	2,5 2 1,5 1 10 1 r s2 мин /s2 опт
Рис. 15	Рис. 16

Дисперсия ошибки в оптимальной системе рассчитана по формуле: