Реферат: Венгерский метод в логистике

Введение 3

1 Задача о назначениях. Венгерский метод 4

1.1 Задача о назначениях 4

1.2 Венгерский метод решения задачи о назначениях 7

2 Решение задачи о назначениях с помощью венгерского метода 15

Заключение 20

Список использованной литературы 21

Введение

Задача о назначениях является частным случаем классической транспортной задачи и, как следствие, является задачей транспортного типа.

Транспортная задача – задача о наиболее экономном плане перевозок однородного или взаимозаменяемого продукта из пункта производства (станций отправления), в пункты потребления (станции назначения) – является важнейшей частной задачей линейного программирования, имеющей обширные практические приложения не только к проблемам транспорта.

Применительно к задаче о назначениях симплексный метод не эффективен, так как любое ее допустимое базисное решение является вырожденным. Специфические особенности задачи о назначениях позволили разработать эффективный метод ее решения, известный как венгерский метод.

1 Задача о назначениях. Венгерский метод

1.1 Задача о назначениях

Предположим, что имеется п различных работ, каждую из которых может выполнить любой из п привлеченных испол­нителей. Стоимость выполнения і-й работы j - м исполнителем известна и равна C_{і j} (в условных денежных единицах). Необхо­димо распределить исполнителей по работам (назначить одного исполнителя на каждую работу) так, чтобы минимизировать суммарные затраты, связанные с выполнением всего комплекса работ.

В исследовании операций задача, сформулированная выше, известна как задача о назначениях. Введем переменные X_ij , где X_ij принимает значение 1 в случае, когда і-ю работу выполняет j-й исполнитель, и значение 0 во всех остальных случаях, i,j = 1, п . Тогда ограничение

гарантирует выполнение каждой работы лишь одним исполни­телем, ограничение

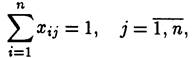
гарантирует, что каждый из исполнителей будет выполнять лишь одну работу. Стоимость выполнения всего комплекса работ равна

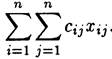
Таким образом, задачу о назначениях можно записать следую­щим образом:

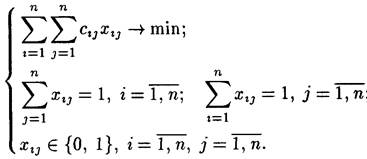
(1)

Задача о назначениях (1) является частным случаем классической транспортной задачи, в которой надо положить При этом условие означает выполнение требова­ния целочисленности переменных x_{і j} . Это связано с тем, что мощности всех источников и стоков равны единице, откуда следует, что в допустимом целочисленном решении значениями переменных могут быть только 0 и 1.

Как частный случай классической транспортной задачи, за­дачу о назначениях можно рассматривать как задачу линейного программирования. Поэтому в данном случае используют тер­минологию и теоретические результаты линейного программи­рования.

В задаче о назначениях переменное х_{і j} может принимать значение 0 или 1. При этом, согласно (1), в любом допусти­мом решении лишь п переменных могут принимать значения 1. Таким образом, любое допустимое базисное решение задачи о назначениях будет вырожденным.

На практике встречаются задачи о назначениях, в поста­новках которых параметр понимается как эффективность выполнения і-й работы j - м исполнителем. В этих случаях нужно так распределить работы между исполни­телями, чтобы суммарная эффективность их выполнения была бы максимальной, т.е.

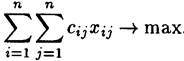(2)

где максимум ищется при ограничениях, указанных в (1).

Параметры задачи о назначениях (1) удобно представлять матрицей , которую называют матрицей стоимости. Предположим, что и С = (c_{і j} ) — две матрицы стоимости, элементы которых связаны следующим образом:

где — некоторые постоянные. Таким образом, для получения матрицы С* нужно к элементам каждой і-й строки матрицы С прибавить число d,-, а к элементам ее каждого j - г o столбца — число Ц. В этом случае, если X — допустимое решение, удовлетворяющее ограничениям из (1), и

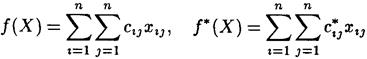
то с учетом ограничений из (1) типа равенства имеем

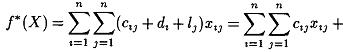
где

Таким образом, для любого допустимого решения X соот­ветствующие ему значения функций будут отличаться на постоянную у, которая не зависит от X . Поэтому, если есть две задачи о назначениях с одним и тем же множеством G допу­стимых решений и целевыми функциями соответственно, то их оптимальные решения совпадают. Нетрудно убедиться в наличии аналогичного свойства и у классической транспортной задачи.

Если задача о назначениях является задачей максимизации, т.е. ищется максимум целевой функции на множестве G допу­стимых решений, которое задается системой ограничений из (1), то эквивалентную ей задачу минимизации

--> ЧИТАТЬ ПОЛНОСТЬЮ <--