Реферат: Вероятностные сетевые модели в средней школе

S2(i,j)

t5(i,j) t4(i,j) t3(i,j) t2(i,j) (0;1) 1 1,5 2 3 1,825 ≈0,38 (1;3) 2 3 4 5 3,5 0,95 (3;5) 0 0 0 0 0 0 (5;7) 1 2 3 4 2,5 0,95 (7;12) 0 0 0 0 0 0 (12; 16) 1,5 2 3 4 2,6 0,69 (16;19) 1,5 2 3 4 2,6 0,69 (19;21) 0 0 0 0 0 0 (21;22) 0 0 0 0 0 0 (22;23) 0 0 0 0 0 0 (23;24) 0,5 1 2 3 1,6 0,69 Всего 14,6 2,1

Полагая t^ случайной величиной, имеющей нормальное распределение, со средним значением tкр=14,6 и средним квадратичным отклонением, равным σ=2,1, получаем, что вероятность того, что общая продолжительность для изучения темы «Многочлены» не превысит, к примеру, T=27, равна

где Ф - интегральная функция Лапласа. Таким образом, вероятность усвоения всей темы в модельном классе не более чем за 27 часов составляет примерно 0,99.

В качестве второго примера рассмотрим изучение темы «Производная» в 10 классе по учебнику «Алгебра и начала анализа, 10-11» [2]. Необходимый перечень умений и навыков приведен в следующей таблице:

Таблица 3

№ п/п	Тема		Продолжительность изучения (час)	Предшествующая тема
	Название темы	Обозначение темы
1	Приращение функции	а1	2	-
2	Понятие производной	а2	2	а1
3	Понятие о непрерывности функции и предельном переходе	а3	2	ai,a2
4	Правила вычисления производных	а4	4	а2
5	Производная сложной функции	а5	2	а2,а4
6	Производные тригонометрических функций	а6	3	а2, а4, а5
7	Применение непрерывности	а7	4	а3
8	Касательная к графику функции	а8	3	а2, а7
9	Производная в физике и технике	а9	2	а8,а2
10	Применение производной к исследованию функции	а1	14	а2, а3, а4, а8, а5,

Полученный сетевой график с расчетом временных характеристик и разбиения на слои выглядит следующим образом:

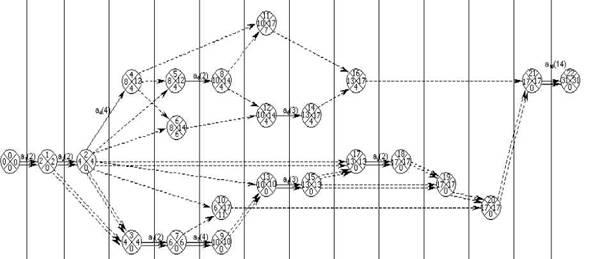
Рис.2. Сетевой график по теме «Производная»

Критический путь состоит из 30 часов и содержит темы:

1) аь а3, а7, а8, а9, а10;

2) а1, а2, а9, а10;

3) аь а2, а3, а7, а8, а9, а10.

Расчет математического ожидания и дисперсии приведен в следующей таблице:

Таблица 4

Раздел (i,j)	Продолжительность				Ожидаемая продолжительность ж(i,j)	Дисперсия S2(i,j)
	t5(i,j)	t4(i,j)	t3(i,j)	t2(i,j)
(0;1)	2	3	4	5	3,5	0,95
(1;2)	1	1,5	2	3	1,825	≈0,38
(2;3)	0	0	0	0	0	0
(3;7)	1	1,5	2	3	1,825	≈0,38
(7;9)	2	3	4	5	3,5	0,95
(9; 13)	0	0	0	0	0	0
(13;15)	1	2	3	4	2,5	0,95
(15;17)	0	0	0	0	0	0
(17;18)	2	3	4	5	3,5	0,95
(18;19)	0	0	0	0	0	0
(19;20)	0	0	0	0	0	0
(20;21)	0	0	0	0	0	0
(21;22)	12	13	14	15	13,5	0,95
Всего	30	5,51

Вероятность того, что максимальный срок, необходимый для усвоения темы, не превысит, к примеру, 28 часов, равна:

то есть вероятность усвоения всей темы в модельном классе не более чем за 28 часов составляет примерно 0,21.

Список литературы

1. Карасев А.И., Кремер Н.Ш., Савельева Т.И. Математические методы и модели в планировании: Учебное пособие. М.: Экономика, 1987.

2. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа 10-11/ Под ред. А.Н.КолмогороваМ.: Просвещение, 1990.

3. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра - 7/ Под ред. С.А. Теляковского М.: Просвещение, 1991.

4. Половников В.А., Орлова И.В., Федосеев В.В., Гармаш А.Н. Экономико-математические методы и модели. М.: Финстатинформ, 1997.

5. Таха Х. Введение в исследование операций. М., 1985.