Реферат: Вопросы устойчивости и общие сведения об автогенераторах

Это один из наиболее простых и эффективных критериев устойчивости. Суть его заключается в следующем. Электрическая цепь будет устойчивой, если при изменении переменной w от 0 до ¥ аргумент j_N (w) полинома N (j w) знаменателя операторной передаточной функции Т (р ) возрастает на угол 0,5pn радиан, где n – степень полинома N (р ). В практических случаях часто удобнее пользоваться геометрической трактовкой этого критерия: электрическая цепь будет устойчивой, если годограф N (j w) при изменении частоты от 0 до ¥, начиная с вещественной оси комплексной плоскости (а _n ¹ 0, т. е. начальная точка годографа при w = 0 не должна быть нулевой), последовательно обходит n квадрантов в положительном направлении, т. е. против часовой стрелки.

Пример 8.2.

Пусть дана электрическая цепь второго порядка с характеристическим уравнением

Пользуясь критерием Михайлова оценить устойчивость.

Решение задачи.

Заменим р на j w и получим

Вычислим вещественную и мнимую части N (j w) для нескольких значений w и сведем полученные результаты в таблицу 8.1.

Таблица 8.1.

w	0	1	2	3	4	¥
Re [N (j w)]	1	0	–3	–8	–15	–¥
Im [N (j w)]	0	1	2	3	4	¥

Изобразим годограф N (j w) на комплексной плоскости (рис. 8.2).

Очевидно, что с ростом частоты w конец вектора N (j w) последовательно проходит два квадранта, начиная с первого. Следовательно, согласно критерию Михайлова, цепь устойчива.

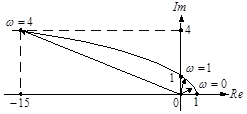
Рис. 8.2. Построение годографа полинома знаменателя

Пример 8.3.

Пусть электрическая цепь описывается передаточной функцией

где

Оценить устойчивость электрической цепи.

Решение задачи.

Заменим р на j w и получим

Используя критерий Михайлова, построим годограф функции N (j w), давая последовательно значения частоты w от 0 до ¥ (рис. 8.3):

Рис. 8.3. Годограф функции N (j w)

Очевидно, что в данном случае электрическая цепь не является устойчивой, так как конец вектора из первого квадранта переходит в четвертый и затем в третий, т. е. нарушается последовательность обхода, хотя общее число квадрантов, в которых побывал конец вектора, равно трем, т. е. совпадает с порядком характеристического уравнения N (р ).

Критерий Найквиста. Этот критерий, как и критерий Михайлова, является частотным (в отличие от алгебраического критерия Гурвица). Он позволяет судить об устойчивости усилителя с обратной связью по виду частотной характеристики данного усилителя при разомкнутой цепи ОС. Суть критерия состоит в следующем. Система с ОС устойчива, если годограф разомкнутой системы не охватывает точку на комплексной плоскости с координатами (1, j 0). В противном случае система будет неустойчива и может рассматриваться как автогенератор.

Рассмотрим критерий подробнее. На рисунке 8.4 показана схема усилителя с ОС.