Реферат: Вычисление интеграла методом Ньютона-Котеса (теория и программа на Паскале)
2)Найдем значения y:
| x0=0 | y0=1 |
| x1=1 | y1=0.5 |
| x2=2 | y2=0.2 |
| x3=3 | y3=0.1 |
| x4=4 | y4=0.0588 |
| x5=5 | y5=0.0384 |
| x6=6 | y6=0.0270 |
| x7=7 | y7=0.02 |
3) Находим коэффициенты Ньютона-Котеса:
H1=H7=0.0435, H1=H6=0.2040, H2=H5=0.0760 ,H3=H4=0.1730
Подставим значения в формулу и получим:
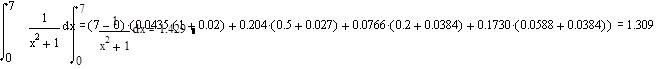
При подсчете с помощью формулы Ньютона-Лейбница получим:
Пример 2.
Вычислить при помощи метода Ньютона-Котеса
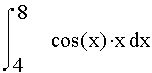 , взяв n=5;
, взяв n=5;
Вычисление:
1) Определим шаг h=(8-4)/5=0.8
2) Найдем значения y:
| x0=0 | y0=-2.61 |
| x1=4.8 | y1=0.42 |
| x2=5.6 | y2=4.34 |
| x3=6.4 | y3=6.35 |
| x4=7.2 | y4=4.38 |
| x5=8 | y5=-0.16 |
3) Находим коэффициенты Ньютона –Котеса:
H0=H5=0.065972 ;H1=H4=0.260417 ;H2=H3=0.173611 ;
4)Подставим значения в формулу и получим:
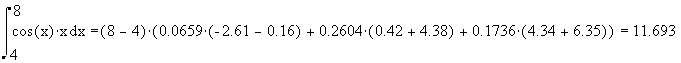
Рассмотрим частные случаи формулы Ньйтона-Котеса.
Пусть n=1 тогда
H0=H1=0.5 и конечная формула примет вид:
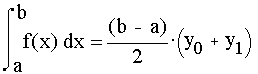 Тем самым в качестве частного случая нашей формулы мы получили формулу трапеций.
Тем самым в качестве частного случая нашей формулы мы получили формулу трапеций.
Взяв n=3, мы получим
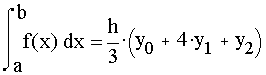 . Частный случай формулы Ньютона –Котеса – формула Симпсона
. Частный случай формулы Ньютона –Котеса – формула Симпсона
![]()
Теперь произведем анализ алгоритма и рассмотрим основной принцип работы программы.
Для вычисления интеграла сначала находятся коэффициенты Ньютона-Котеса. Их нахождение осуществляется в процедуре hkoef.
Основной проблемой вычисления коэффициентов является интеграл от произведения множителей. Для его расчета необходимо:
А) посчитать коэффициенты при раскрытии скобок при q
(процедура mnogoclen)
Б) домножить их на 1/n , где n –степень при q (процедура koef)
В) подставить вместо q значение n (функция integral)