Реферат: Вынужденные колебания. Амплитудно-частотные и фазово-частотные характеристики

Колебания – такие процессы, при которых параметры, характеризующие состояние колебательной системы, повторяются с течением времени. Например, колебания маятника в маятниковых часах, суточные колебания освещённости данного участка Земной поверхности и т.д.

Вынужденные колебания - колебания системы, возникающие под воздействием внешней вынуждающей силы. Характер этих колебаний опре­деляется как свойствами самой колебательной системы, так и внешней силой. Обычно принимают, что внешняя периодическая сила изме­няется по гармоническому закону .

Рис. 1 Система с вынужденными колебаниями

Рис. 2 Силы, действующие в системе

Рассмотрим колебательную систему, показанную на рисунке 1.

Она состоит из горизонтального пружинного маятника и кривошипо-шатунного механизма. Кривошипо-шатунный механизм - механизм, который преобразует вращательное движение в возвратно-поступательное.

Тогда II-й закон Ньютона для данной системы запишется в виде:

,

(1)

где - масса тела, – его ускорение, - сила тяжести, - сила реакции опоры, - сила вязкого трения (), - внешняя вынуждающая сила, - сила упругости пружины ().

В проекции на ось x :

(2)

введём замены: , , получим:

(3)

Введём обозначения ( – показатель затухания, - коэффициент сопротивления), ( – циклическая частота свободных колебаний системы в отсутствие трения), – приведённая сила. Тогда можем переписать уравнение в общем виде:

(4)

Уравнение (4) – дифференциальное уравнение вынужденных колебаний, линейное, второй степени, неоднородное (с правой частью). Исследуем его. Как известно из теории дифференциальных уравнений, решением уравнения (4) является сумма двух решений: общего решения однородного уравнения соответствующего данному неоднородному и частного решение неоднородного уравнения в целом.

Однородное уравнение соответствующее данному неоднородному есть уравнение затухающих колебаний

1.

2.

3.

4.:

a.

(5)

Решением этого уравнения является функция:

, где .

(6)

Частное решение неоднородного уравнения в целом будем искать следующим образом. Как показывает практика, не зависимо от начальных условий осциллятора через достаточно большой промежуток времени (время разгорания/релаксации) в системе установятся гармонические колебания с частотой вынуждающей силы и амплитудой , зависящей от частоты .

Различные случаи установления гармонических колебаний:
Рис. 3 Случай разгорания для	Рис. 4 Произвольный случай разгорания

Здесь – это время разгорания колебаний.

Это значит, что через достаточно большой промежуток времени первым слагаемым можно пренебречь. Действительно в (6) при ,. Таким образом

,

(7)

где - амплитуда установившихся колебаний с частотой - частотой внешней вынуждающей силы, - сдвиг фаз между смещением и фазой внешней силы.

Найдем, чему равны и при частоте внешней силы . Для этого найдем 1-ю и 2-ю производные от (7):

	(8)
	(9)

И подставим (7), (8), (9) в (4):

,

немного преобразуем:

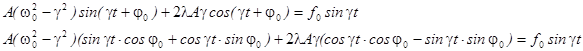
и получим:

Данное уравнение будет справедливо при любом , если коэффициенты при и будут равны нулю:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--