Реферат: Вывод уравнения Шредингера

Уравнение Шрёдингера, как это требовалось с самого начала для выполнения принципа суперпозиции, линейно и однородно относительно функции Ψ. В точной математической форме принцип суперпозиции сводится к двум утверждениям.

Во-первых, если Ψ1 и Ψ2 — какие-либо два решения уравнения Шрёдингера, то и всякая линейная комбинация их α1Ψ1 + α2Ψ2 с постоянными (вообще говоря, комплексными) коэффициентами α1 и α2 есть также решение того же уравнения. Во-вторых, если волновые функции Ψ1 и Ψ2 описывают какие-либо два состояния системы, то и линейная комбинация α1Ψ1 + α2Ψ2 также описывает какое-то состояние той же системы. Конечно, состояние частицы определяется не самими коэффициентами α1 и α2, а только их отношением α1/α2 . Состояние не изменится, если оба коэффициента умножить на одну и ту же вещественную или комплексную постоянную. Это позволяет, например, функцию Ψ = α1Ψ1 + α2Ψ2 нормировать (если интеграл , взятый по всему пространству, сходится).

Особое значение в квантовой механике имеют стационарные состояния. Это – такие состояния, в которых все наблюдаемые физические параметры не меняются с течением времени. Сама волновая функция Ψ не относится к этим параметрам. Она принципиально не наблюдаема. Не должны меняться во времени только физически наблюдаемые величины, которые могут быть образованы из Ψ по правилам квантовой механики.

Как следует из уравнения (9), вид волновой функции Ψ определяется потенциальной энергией U, т. е., в конечном счете, характером тех сил, которые действуют на частицу. Вообще говоря, U есть функция координат и времени. Для стационарного (не меняющегося со временем) силового поля U не зависит явно от времени. В последнем случае волновая функция Ψ распадается на два множителя, один из которых зависит только от времени, второй – только от координат:

(10)

(Е — полная энергия частицы, (E/ħ) = ω ).

Учтём, что дифференциал (11)

Подстановка функции (10) в уравнение (9) с учётом (11) дает:

Сокращая все члены этого уравнения на общий множитель e-i(E/ħ)t и произведя соответствующие преобразования, получим дифференциальное уравнение, определяющее функцию ψ:

(12)

Если функция U зависит от времени явно, то и решение последнего уравнения – функция ψ – будет зависеть от времени, что противоречит предположению (10).

Уравнение (12) называется уравнением Шрёдингера для стационарных состояний (или уравнением Шрёдингера без времени).

К уравнению Шрёдингера можно прийти и следующим путем следующих рассуждений. Из опытов по дифракции микрочастиц вытекает, что параллельный пучок частиц обладает свойствами плоской волны, распространяющейся в направлении движения частиц. Уравнение плоской волны, распространяющейся в направлении оси x, имеет, как известно, вид:

Это выражение часто пишут в комплексном виде:

(13)

подразумевая, что надо принимать во внимание вещественную часть этого выражения.

Согласно гипотезе де Бройля свободному движению частицы соответствует плоская волна с частотой ω=Е/ħ и длиной волны λ = 2πħ/р. Заменяя ω и λ в выражении (13) соответствующими выражениями, получим волновую функцию для свободной частицы, движущейся в направлении оси х:

(14)

Чтобы найти дифференциальное уравнение, которому удовлетворяет функция (14), воспользуемся соотношением между Е и p:

E= p2/2m. (15)

Продифференцировав функцию (14) один раз по t, a второй раз дважды по x, получим:

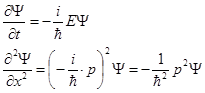
Из этих соотношений можно выразить Е и р2 через функцию Ψ и ее производные:

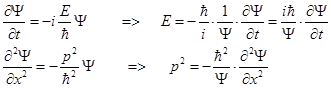
Как видим прослеживается полная аналогия с (7*). Подставляя полученные выражения в соотношение (15) получим дифференциальное уравнение:

Если направление волны не совпадает с осью х (или у, или z), фаза колебаний будет зависеть от всех координат: х, у и z. В этом случае дифференциальное уравнение имеет вид: