Реферат: Взаємодія елементарних частинок з речовиною

де Ra – пробіг у см; Ea – кінетична енергія a – частинок у МеВ .

Для a – частинок природних a – випромінювачів (4 МеВ < Ea < 9 МеВ), В = 0.318 , n = 1.5. Для a – частинок з більш високими енергіями Е_а ≥ 200( МеВ) В = 0.148 , n = 1.8. Так, a – частинки з енергіями Ea = 5 МеВ пробігають у повітрі відстань 3.51 см, а з енергією Ea = 30 МеВ – 68 см. Відношення лінійних пробігів двох типів частинок, які розпочинають рух у повітрі з однаковими швидкостями, пропорційний відношенню питомих втрат енергії цих частинок:

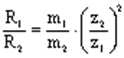, (3.5.2.2)

де m₁ і m₂ – відповідно, маси частинок; z₁ і z₂ – зарядові числа частинок.

Часто замість лінійного пробігу використовують масовий пробіг зарядженої частки R_m , який виражається у грамах на квадратний сантиметр (г/см² ). Чисельно масовий пробіг дорівнює масі речовини, яка розміщена в циліндрі, висота якого дорівнює лінійному пробігу частинки R у сантиметрах, з площею поперечного перерізу – 1 см² .

, (3.5.2.3)

де ρ – густина речовини в г/см³ .

Масовий пробіг зарядженої частинки зручний тим, що він мало залежить від хімічного складу речовини.

3.5.3 Взаємодія бета-частинок з речовиною

При русі в речовині легкі заряджені частинки втрачають свою енергію. Ці втрати можна поділити на іонізаційні й радіаційні.

При русі легких заряджених частинок у речовині питомі іонізаційні втрати зменшуються із збільшенням їх швидкості до кінетичних енергій, які дорівнюють подвоєний енергії спокою електрона, а потім повільно зростають.

Радіаційні втрати спостерігаються при прискореному русі вільних заряджених частинок в електричному полі ядра. Пролітаючи поблизу ядра, заряджена частинка відхиляється від свого попереднього напрямку під дією кулонівської сили F. Ця сила пов'язана з масою частинки m і її прискоренням a другим законом Ньютона F = ma. Вільний заряд, який рухається з прискоренням a , випромінює електромагнітні хвилі, енергія яких пропорційна порядковому номеру елемента. Оскільки кулонівська сила пропорційна порядковому номеру елемента в таблиці Менделєєва z, то a² ~ z² /m² . Отже, радіаційні втрати важких заряджених частинок значно менші радіаційних втрат електронів і позитронів. Із збільшенням енергії електронів їх електричне поле в перпендикулярному напрямку підсилюється, тому радіаційні втрати ростуть пропорційно до зростання кінетичної енергії електронів Е_е- . Отже, питомі радіаційні втрати енергії Е_е- пропорційні енергії і квадрату порядкового номера речовини:

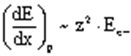. (3.5.3.1)

Іонізаційні втрати в електронів переважають в області порівняно невеликих енергій. Із збільшенням кінетичної енергії внесок іонізаційних втрат у загальних втратах енергії зменшується. Оскільки питомі іонізаційні втрати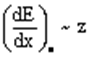 , то відношення питомих радіаційних і іонізаційних втрат k енергії пропорційне , тобто

, (3.5.3.2)

тут Е_е- береться у МеВ.

Енергію електронів , при якій питомі іонізаційні і радіаційні втрати рівні (k = 1), називають критичною . Критична енергія для заліза (z = 26) дорівнює 31 МеВ, а для свинцю (z = 82) - приблизно 9.8 МеВ. Практичний інтерес має не дійсний лінійний пробіг, а ефективний . Він дорівнює товщині шару речовини, яка повністю поглинає електрони. Ефективні масові пробіги R_me моно енергетичних електронів знаходять за емпіричними формулами:

для

для (3.5.3.3)

де R_me вимірюють у грамах на квадратний сантиметр (г/см² ); E_е - кінетична енергія електронів у МеВ.

3.5.4 Взаємодія нейтронів з речовиною

Нейтрони, пролітаючи крізь речовину, безпосередньо не іонізують атоми й молекули, подібно до заряджених частинок. Тому нейтрони виявляють за допомогою вторинних ефектів, які виникають при взаємодії їх з ядрами. У результаті зіткнення нейтронів з ядрами речовини, природа останніх не змінюється, а самі нейтрони розсіюються на атомних ядрах.

Зіткнення нейтронів з ядрами можуть бути пружними й не пружними. При непружних взаємодіях відбуваються ядерні реакції типу (n, a ), (n, p ), (n, γ ), (n, 2n ) і т.д., і спостерігаються ядерні реакції поділу важких ядер.

Імовірність проходження тієї чи іншої ядерної реакції визначається мікроскопічним перерізом реакції σ(n, a), σ(n, p), σ(n, y), σ(n, 2n) і т.д. (першою в дужках записується частинка, яка бомбардує нейтрон, другою – частинка, що випускається, або γ-квант).

Мікроскопічний переріз σ можна уявити як перетин сфери, описаної навколо ядра. Перетинаючи сферу, нейтрон може вступити в реакцію з ядром. Поза сферою радіусом взаємодії не відбуваються. Мікроскопічний переріз виміряється в квадратних сантиметрах (см² ) і барнах (1барн = 10^-24 см² ). Експериментально доведено, що при енергіях нейтронів, більших за 10 МеВ, повний ефективний переріз дорівнює :

, (3.5.4.1)

де R - радіус ядра.

Звідси радіус ядра дорівнює

R = (3.5.4.2)

Більш точні експериментальні вимірювання радіуса ядра R в залежності від масового числа A були проведені з використанням нейтронів з енергіями 14 і 25 МеВ. Вимірювання показали, що

R = (1,3 ÷1,4)·10^-15 A^1/3 м. (3.5.4.3)

Помноживши мікроскопічний переріз σ на число ядер у 1 см³ поглинаючої речовини N, одержимо повний переріз усіх ядер у 1 см³ поглинаючої речовини. Макроскопічний переріз Σ в цьому випадку дорівнює: