Реферат: Задача о бесконечной ортотропной пластинке
Подставляя полученные перемещения в неиспользованные соотношения уравнений Коши, и приравнивая к 0 сомножители при степенях x3 , получим:
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
Исходя из того, что:
![]()
функция D будет иметь вид:
![]() (14)
(14)
Тогда с учетом системы (7) получим:
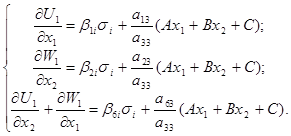 (15)
(15)
Исключая V1 , U1 , W1 ( путем дифференцирования, сложения и вычитания) получим:
![]() (16)
(16)
![]() (17)
(17)
Подставляя в уравнения (16) и (17) выведенные нами выражения для напряжений через функции F(x1 ,x2 ) и y(x1 ,x2 ) и группируя получим:
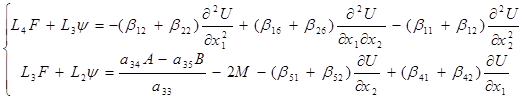 (18)
(18)
где L4 , L3 , L2 - дифференциальные операторы в частных производных 4-го, 3-го и 2-го порядков:
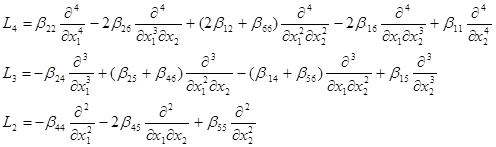
Уравнения (18) представляют собой систему 2-х дифференциальных уравнений в частных производных. Уравнения - линейные, неоднородные, с постоянными коэффициентами.
Общее решение системы (18) для функций напряжения можно представить в виде:
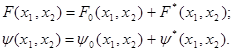
F0 и y0 - общее решение соответствующей однородной системы:
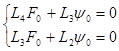 (19)
(19)
F* и y* - частные решения неоднородной системы уравнений (18). Частные решения зависят от правых частей уравнений и если эти правые части несложны, то и частные решения обычно описать нетрудно.
Чтобы получить общее решение однородной системы (19) исключим из нее y0:
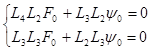 (20)
(20)
В силу симметрии L их можно менять местами:
![]() (21)
(21)
Таким образом, мы получили линейное дифференциальное уравнение 6-го порядка для функции F. Аналогично находим уравнение для y:
![]() (22)
(22)
Оказалось, что F0 и y0 должны удовлетворять одинаковым условиям. Оператор 6-го порядка можно разложить на 6-ть линейных операторов 1-ого порядка Dk и уравнение (21) представить в виде:
![]() (23)
(23)
Из теории диф. уравнений и условия что функция F0 зависит только от x1 и x2 для Dk имеем:
![]() (24)
(24)
где ![]() - это корни алгебраического (характеристического) уравнения шестой степени, соответствующего дифференциальному уравнению (21).
- это корни алгебраического (характеристического) уравнения шестой степени, соответствующего дифференциальному уравнению (21).
Интегрирование линейного уравнения 6-го порядка можно свести к последовательному интегрированию шести уравнений первого порядка. В результате получим следующие общие выражения:
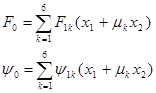
Если среди корней характеристического уравнения есть кратные, задача упрощается, однако решение системы (19) может быть найдено в любом случае исходя из следующих рассуждений.
Любые 6 вещественных чисел можно принять в качестве значений независимых компонент тензора напряжений в данной точке упругого анизотропного тела. Удельная потенциальная энергия деформации есть величина положительная при любых вещественных и не равных нулю значениях компонент тензора напряжений в данной точке. Исходя из этих предположений можно доказать теорему, согласно которой алгебраическое характеристическое уравнение системы (21), не имеет вещественных корней. Поэтому можно утверждать, что числа ![]() в общем решении системы (19), а также в условиях связи всегда комплексные или чисто мнимые.
в общем решении системы (19), а также в условиях связи всегда комплексные или чисто мнимые.
Наряду с комплексными параметрами вводят и систему комплексных переменных:
![]()
Введение комплексных переменных позволяет использовать при аналитическом решении рассматриваемой задачи об упругом равновесии анизотропного тела математический аппарат и методы функций комплексных переменных. Эти методы, применительно к данной задаче являются очень эффективными и позволяют получить аналитическое решение многих плоских задач теории упругости анизотропного тела.
2. Прикладная часть
2.1 Физическая постановка задачи.
 | |
?????????? ??????????? ????????? ?? ???????????? ????????? ? ????????????? ?????????? ? ??????. ??????????? ??????? ???? ??????? ????????? ? ???????? ????? ????????? ?????????, ?????? ????????? ?? ????????????? ????? ??????? ????.
Введем следующие обозначения 2a, 2b - главные оси эллипса, с=a/b, р - усилие на единицу площади. В нашем случае отношение полуосей эллипса с=1/2. Вдоль оси 1 на бесконечности приложено растягивающее усилии р, а вдоль оси 2 - сжимающее -р. Наша задача найти напряжения на краю отверстия и построить их эпюру.
2.2 Упругие свойства материала.
Пластинка сделана из стеклопластика C-II-32-50 со следующими характеристиками:
Е1 =13,0 ГПа;
Е2 =19,8 ГПа;
Е3 =7,8 ГПа;
G12 =4,05 ГПа;
G13 =6,4 ГПа;