Реферат: Задача остовных деревьев в k–связном графе

Такое ребро (1.4) будет называться петлей . При изображении графа петля будет представляться замкнутой дугой, возвращающейся в вершину а и не проходящей через другие вершины (рис 1.5). Петля обычно считается неориентированной. Можно расширить полный граф U в (1.3) до полного графа с петлями U ₀ , добавляя

петлю в каждой вершине, так что ребрами U ₀ являются все пары (1.2), где допускается и a = b .

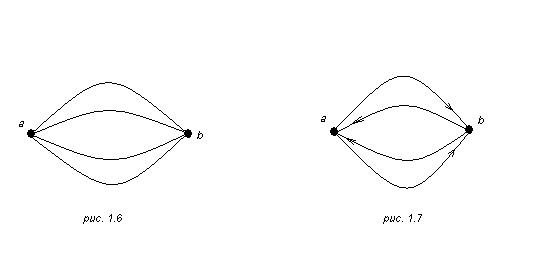
Во–вторых, можно расширить понятие графа, допуская, чтобы пара вершин соединялась несколькими различными ребрами

E_i =(a, b)_i , (1.5)

как это изображено на рис. 1.6. Для ориентированного графа две вершины a и b могут соединяться несколькими ребрами в каждом из направлений:

E_i =(a, b)_i , =(a, b)_j ,

(рис. 1.7).

Чтобы проиллюстрировать случай, для которого эти понятия оказываются естественными, рассмотрим какое–либо командное соревнование, например турнирную таблицу лиги бейсбола. Вершинами соответствующего графа

являются команды. Пара команд А и В связывается ребром каждый раз, когда они сыграли. Если А выиграла у В , то это ребро будем ориентировать от А к В . а если В выиграла у А , то противоположном направлении; в случае ничьей ребро будет неориентированным.

Для каждого графа G существует обратный граф G ^* , получаемый изменением ориентации каждого из ребер G на противоположную. Для

каждого ориентированного графа существует также соотнесенный неориентированный граф G_u , ребрами которого являются ребра G , но уже без ориентаций. Иногда удобно превратить неориентированный граф G в ориентированный граф G_d при помощи процесса удвоения , состоящего в замене каждого ребра G парой с теми же концами и приписывании им противоположных ориентаций.

Граф называется плоским , если он может быть изображен на плоскости так что все пересечения ребер являются вершинами G . Граф на рис 1.8а плоский, а на рис 1.8б неплоский.

§2. Матрицы смежности и инцидентности.

В § 1 мы определили ребро Е (1.2) графа G (1.1) как элемент или точку ( a , b ) в произведении V ´ V . Как обычно, элементы этого произведения можно представить в виде клеток квадратной таблицы М с элементами множества V в качестве координат по двум осям (рис 2.1).

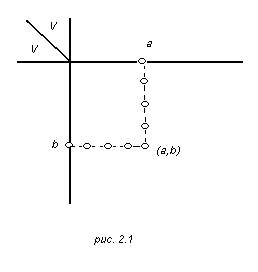В точку с координатами ( a , b ) поместим числа 1 или 0 в зависимости от того, существует или не существует в G соответствующее ребро. Таким образом, мы получили конечную или бесконечную матрицу смежности (вершин ) М( G ) , которая полностью описывает G , если имеет однократные ребра. Обычно обозначения выбираются так, чтобы элементы (а, а), соответствующие петлям, располагались на главной диагонали матрицы М . Если G –неориентированный граф, то ребра ( a , b ) и ( b , a ) существуют одновременно, таким образом, неориентированным графам соответствуют симметрические матрицы смежности.

Если G имеет кратные ребра, то числа 0 и 1 в клетках ( a , b ) можно заменить кратностями r ( a , b ) ребер, соединяющих а и b . Это дает описание графа G матрицей с целыми неориентированными элементами. Обратно, любая такая матрица может быть интерпретирована как граф, так что любые результаты для графов могут быть сформулированы как свойства таких матриц.

Сказанное приводит к дальнейшему расширению понятия графа, использующему уже все конечные или бесконечные матрицы, элементами которых являются вещественные неотрицательные числа. Такие матрицы встречаются в различных областях математики. Например, стохастические матрицы – в теории вероятностей и в теоретической физике. Где рассматриваемая система имеет некоторое множество V возможных состояний, и любая пара состояний ( a , b ) связывается некоторой вероятностью перехода r ( a , b ). Другим примером является граф, представляющий схему дорог, в котором r ( a , b ) означает соответствующее расстояние между а и b .

Графы могут быть также описаны матрицами другого вида. Всякий граф состоит из объектов двух типов–вершин и ребер. Можно построить матицу M ₁ ( G ), строки которой соответствуют вершинам, а столбцы–ребрам. На месте (а, Е) в этой матрице поместим значение e =1 , если а –начальная вершина ребра Е, значение e =-1 , если а –конечная вершина, и e =0 , если а не инцидентно Е. Если G –неориентированный граф, то можно использовать только значения e =1 и e =0 . Эта матрица M ₁ ( G ) называется матрицей инцидентности графа G .

Введем, наконец, матрицу смежности ребер I ( G ), в которой и строки и столбцы отвечают ребрам G . Для простоты предположим. Что G не имеет петель, а ребра неориентированные и однократные. На месте ( E , E ’ ) в I ( G ) поместим e =1 , если Е и Œ –различные ребра с общим концом, и e =0 , если Е=Е’ или если они не имеют общего конца. Таким образом, I ( G )– квадратная матрица, определяемая графом G .

Можно встать и на другую точку зрения и рассматривать I ( G ) как матрицу смежности вершин для нового графа, также обозначаемого через I ( G ), вершинами которого являются ребра Е графа G , а ребрами–пары ( E , E ’) с e =1 . Назовем I ( G ) графом смежности ребер или смежности графом для G . Существование такого графа, в котором бывшие ребра становятся вершинами и наоборот, объясняет двойственность между вершинами и ребрами, встречающуюся в некоторых вопросах теории графов.

Фактическое построение смежности графа I ( G ) по чертежу графа G просто. На каждом ребре Е выбираем фиксированную точку е_Е , например середину Е . Пару таких вершин (е, е’) соединяем новым ребром, принадлежащим I ( G ), тогда и только тогда, когда соответствующие ребра Е и Œ имеют общую вершину в G .

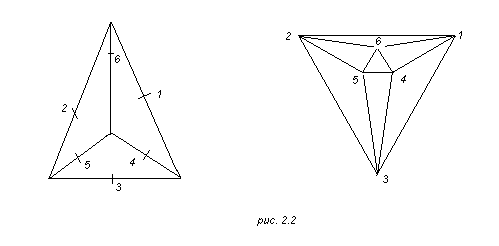
Рис. 2.2 дает это построение для графа тетраэдра; смежностным графом для него является граф октаэдра.

Предположим, то в вершине е сходится r (е) ребер Е=(е, е’) из G . Тогда в I ( G ) середина e_E ребра Е соединяется ребрами с r (е)–1 серединами остальных ребер из G , имеющих конец в е . Таким образом, вI ( G ) эти новые ребра образуют новый граф U ( e ) сr (е) вершинами. В I ( G ) вершина e_E соединяется ребрами также с r (е’)–1 серединами остальных ребер из G, из имеющих конец в e’, и эти новые ребра образуют другой полный граф U ( e ’). Два графа U ( e ) и U ( e ’) имеют ровно одну общую вершину, именно вершину e_E , определяемую единственным ребром Е , соединяющим e и e ’ . Таким образом, I ( G ) имеет такое непересекающееся по ребрам разложение

I ( G )= 2.1

На полные графы U ( e ) с r (е) вершинами, что U ( e ) имеет единственную общую вершину с каждым из r (е) других полных графов U ( e ’). Исключение составляет случай, когда ( e , e ’)– единственное ребро в e ’ , т.е.r (е’)=1. Тогда не существует графа. U ( e ’).

Предположим, что, наоборот, для графа G ₁ существует такое разложение (2.1) на полные графы, что пара ( U ( e ), U ( e ’)) имеет не более одной общей вершины. Тогда G₁ можно рассматривать как смежностный граф G ₁ = I ( G ) некоторого графа G , считая, что каждое U ( e ) имеет r ₁ r (е) общих вершин с другими U ( e ’). Каждому U(e) поставим в соответствие одну вершину e и соединим e и e ’ ребром в G тогда и только тогда, когда U ( e ) и U ( e ’) имеют общую вершину. К этим ребрам добавим r (е)– r ₁ ребер ( e , e ’’), идущих к новым вершинам e ’’ , в которых существует только одно это ребро.

§3 Деревья

Деревом называется связный граф, не содержащий циклов. Любой граф без циклов называется ациклическим (или) лесом . Таким образом, компонентами леса являются деревья. На рис.12 изображены все деревья шестого порядка.

Существует несколько вариантов определения дерева; некоторые из них отражены в следующей теореме.

Теорема 3.1 Для графа следующие утверждения эквивалентны:

1) G – дерево;

2) G – связный граф и m = n -1;

3) G – ациклический граф и m = n -1;