Реферат: Задача остовных деревьев в k–связном графе
работу выполнил
ст. V курса гр.52MI
Жуков В.
Работу приняла:
Dr.физ–мат. наук
Присэкару В.К.
Кишинев–2002
Содержание:
Введение………………………………………………………………………….2
Глава I Основные определения………………………………………………….4
§1 Основные определения теории графов……………………………………...4
§2 Матрицы смежности и инцидентности……………………………………..10
§3 Деревья………………………………………………………………………..13
Глава II Связность ………………………………………………………………18
§4 Вершинная связность и реберная вязность…………………………………18
§5 Двусвязные графы…………………………………………………………....22
§6 Теорема Менгера………………………………………………………….….32
Глава III Выделение k непересекающихся остовных деревьев
2k–реберно связном графе………………………………………………………36
§7 Построение k непересекающихся остовных деревьев………...………...…37
§8 Необходимость условия ![]() (G)
(G)![]() 2k ……………………………………..….40
2k ……………………………………..….40
§9 Текст программы……….………………………………………………….…42
Вывод……………………………………………………………………………..51
Введение
Начало теории графов как математической дисциплины было положено Эйлером в его знаменитом рассуждение о Кенигсбергских мостах. Однако эта статья Эйлера 1736 года была единственной в течение почти ста лет. Интерес к проблемам теории графов возродился около середины прошлого столетия и был сосредоточен главным образом в Англии. Имелось много причин для такого оживления изучения графов. Естественные науки оказали свое влияние на это благодаря исследованиям электрических цепей, моделей кристаллов и структур молекул. Развитие формальной логики привело к изучению бинарных отношений в форме графов. Большое число популярных головоломок подавалось формулировкам непосредственно в терминах графов, и это приводило к пониманию, что многие задачи такого рода содержат некоторое математическое ядро, важность которого выходит за рамки конкретного вопроса. Наиболее знаменитая среди этих задач–проблема четырех красок, впервые поставленная перед математиками Де Морганом около 1850 года. Никакая проблема не вызывала столь многочисленных и остроумных работ в области теории графов. Благодаря своей простой формулировке и раздражающей неуловимости она до сих пор остается мощным стимулом исследований различных свойств графов.
Настоящее столетие было свидетелем неуклонного развития теории графов, которая за последние десять – двадцать лет вступила в новый период интенсивных разработок. В этом процессе явно заметно влияние запросов новых областей: теории игр и программирования, теории передачи сообщений, электрических сетей и контактных цепей, а также проблем психологии и биологии.
Вследствие этого развития предмет теории графов является уже обширным, что все его основные направления невозможно изложить в одном томе. В настоящем первом томе предлагаемого двухтомного труда сделан акцепт на основные понятия и на результаты, вызывающие особый систематический интерес.
По теории графов имеется очень мало книг; основной была книга Д. Кёнига (1936), которая для своего времени давала превосходнейшее введение в предмет. Довольно странно, что таких книг на английском языке до сих пор не было, несмотря на то, что многие важнейшие результаты были получены американскими и английскими авторами.
Глава I
Основные понятия
§1 Определения.
Предметом первых задач в теории графов были конфигурации, состоящие из точек и соединяющих их линий. В этих рассмотрениях было несущественно, прямые ли это линии или же они являются криволинейными непрерывными дугами, соединяющими две концевые точки, где расположены эти линии, являются ли они длинными или короткими. Существенно только то, что они соединяют две данные точки.
Это приводит к определению графа как абстрактного математического понятия. Рассматривая множество V , состоящее из соединенных некоторым образом точек. Назовем V множеством вершин и элементы v![]() V –вершинами . Граф
V –вершинами . Граф
G = G ( V ) (1.1)
c множеством вершин V есть некоторое семейство сочетаний, или пар вида
E=(a, b), a,b![]() V (1.2)
V (1.2)
указывающие, какие вершины являются соседними. В соответствии с геометрическим представлением графа каждая конкретная пара (1.2) называется ребром графа; вершины a и b называются концевыми точками , или концами ребра.
Можно использовать и другой подход. Если даны два множества V 1 и V 2 то можно образовать множество всех пар
(v1 ,v2 ), v1 ![]() V1 , v2
V1 , v2 ![]() V2 .
V2 .
Это множество пар называется произведением и обозначается через V 1 ´ V 2 . В нашем случае каждая пара вершин ( a , b ) есть элемент произведения V ´ V . Таким образом можно сказать, что граф G из (1.1) с данными ребрами (1.2) есть некоторое подмножество произведения V ´ V .
Это определение графа должно быть дополнено в одном важном отношении. В определении ребра (1.2) можно принимать или не принимать во внимание порядок расположения двух его концов. Если этот порядок несуществен, т.е. если
E=(a, b)=(b, a),
то говорят, что Е есть неориентированное ребро ; если же этот порядок существен, то Е называется ориентированным ребром . В последнем случае а называется также начальной вершиной , а b –конечной вершиной ребра Е . Можно также говорить, что Е есть ребро, выходящее из вершины а (отходящее от вершины а , исходящее из вершины а ) и входящее в вершину b (подходящее к вершине b , заходящее в вершину b ). Как в случае ориентированного, так и в случае неориентированного ребра говорят, что ребро Е из (1.2) инцидентно вершинам a и b , а также что а и b инцидентны Е .
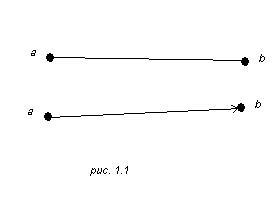
В приложениях граф обычно интерпретируется как сеть , в которой вершинами G являются узлы . Два узла a и b соединяются непрерывной кривой (в частности прямолинейны отрезком) тогда и только тогда, когда имеется пара (1.2). На рисунках узлы будут обозначаться маленькими кружками, а ориентация, если нужно, – стрелкой на представляющей ребро кривой (рис. 1.1).
Граф называется неориентированным , если каждое его ребро не ориентированно, и ориентированным , если ориентированны все его ребра.
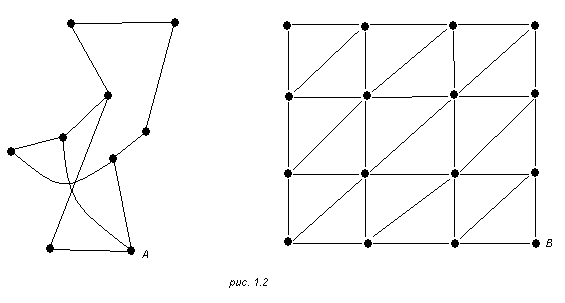
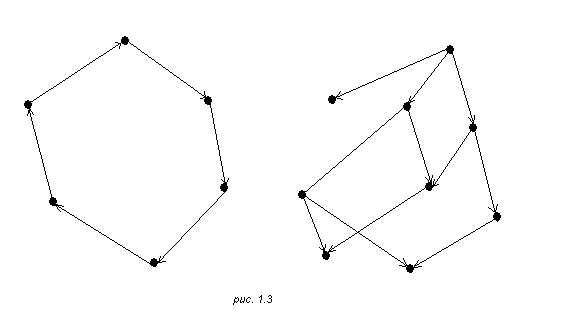
На рис.1.2 приведены примеры неориентированных графов. На рис 1.3 изображены ориентированны графы.
В ряде случаев естественно рассматривать смешанные графы , имеющие как ориентированные, так неориентированные ребра. Например, план города
можно рассматривать как граф, в котором ребра представляют улицы, а вершины – перекрестки; при этом по одним улицам может допускаться лишь одностороннее движение, и тогда на соответствующих ребрах вводится ориентация; по другим улицам движение двустороннее, и на соответствующих ребрах уже никакой ориентации не вводится.
Мы уже отмечали, что при фактическом изображении графа имеется большая свобода в размещении вершин и в выборе формы соединяющих их дуг. Поэтому может оказаться, что один и тот же граф представляется совсем различными чертежами. Будем говорить, что два графа G и G ' изоморфны , если существует такое взаимно однозначное соответствие между множествами их вершин V и V ’ , что вершины соединены ребрами в одном из графов в том и только том случае, когда соответствующие им вершины соединены в другом графе. Если ребра ориентированы, то их направления также должны соответствовать друг другу. На рис 1.2 приведены примеры изоморфных графов, образованных ребрами и вершинами правильных многогранников.
Вершина не инцидентна никакому ребру, называется изолированной . При определение множества вершин V данного графа часто имеет смысл
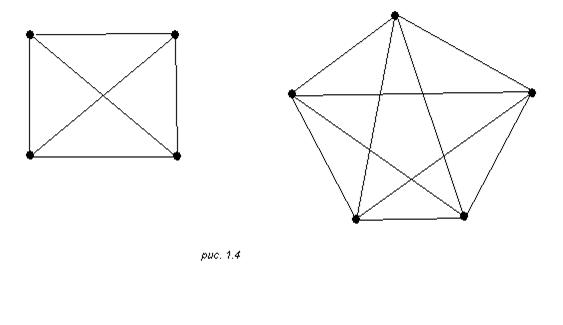
учитывать только неизолированные вершины. Граф, состоящий только из изолированных вершин, называется нуль–графом и может быть обозначен через 0. другим важным случаем является (неориентированный) полный граф
U=U(V) , (1.3)
ребрами которого являются всевозможные пары (1.2) для двух различных вершин a и b из V . На рис. 1.4 даны схемы полных графов для множеств вершин из четырех и из пяти элементов.
В ориентированном полном графе U ( d ) имеются пары ребер, по одному в каждом направлении. Соединяющие любые две различные вершины a и b .
Сформулированное выше определение графа, вместе с соответствующим изображением, достаточно для многих задач. Однако для некоторых целей желательно понятие графа несколько расширить.
 Во–первых, можно получить ребра, у которых обе концевые точки совпадают:
Во–первых, можно получить ребра, у которых обе концевые точки совпадают:
--> ЧИТАТЬ ПОЛНОСТЬЮ <--