Реферат: Задачи оптимизации
Целевая функция имеет вид
![]()
Итак, надо найти ![]() при ограничениях:
при ограничениях:

которая решается графически
Возьмем прямую ![]() и начнем строить параллельные ей в направлении антиградиента, где
и начнем строить параллельные ей в направлении антиградиента, где ![]() .
.
 |
Последняя вершина многоугольника решений есть точка С , получаемая пересечением прямых (1) и (4). Решая, получим С (1;5).
Итак, оптимальные значения будут следующими: ![]() , а общие затраты времени
, а общие затраты времени ![]() (суток).
(суток).
§3 АНАЛИТИЧЕСКИЙ МЕТОД ОПТИМИЗАЦИИ
Пусть дана целевая функция ![]() .
.
Для нахождения наибольшего и наименьшего значения функции и (одной) вещественных переменных надо найти критические точки, в которых частные производные (производная) функции f по всем переменным обращается в 0. Кроме того, надо исследовать точки границы, если она принадлежит области определения. Среди них выбрать значения, где f принимает наибольшее и наименьшее значение.
 Пример 2. Определить оптимальный по времени маршрут выдвижения танкового подразделения из пункта А в пункт F, если допустимая скорость движения танков до дороги
Пример 2. Определить оптимальный по времени маршрут выдвижения танкового подразделения из пункта А в пункт F, если допустимая скорость движения танков до дороги ![]() , по дороге
, по дороге ![]() , за дорогой
, за дорогой ![]() . Удаление от дороге пункта А равно
. Удаление от дороге пункта А равно ![]() , пункта F
, пункта F![]() . Расстояние между точками В и Е равно L = 90 км .
. Расстояние между точками В и Е равно L = 90 км .
Составим математическую модель, то есть найдем функцию цели. Нас интересует время. Время выдвижения из пункта А в пункт F.

ВС = х км ; DE = yкм ; АС = ![]()
CD = L – x – y; DF = ![]()
![]()

Составим функцию цели, которая зависит от двух переменных ![]()
Найдем критические точки
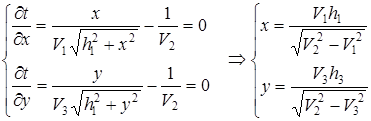
При данных условиях 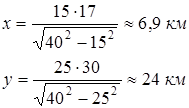
Найдем значение t при полученных x и y
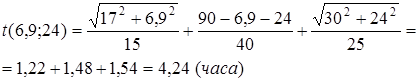
При вычислении значения t на границе, значения получаются больше, чем 4,24 часа. Следовательно, оптимальное решение будет при
х = 6,9 км , у = 24 км , ![]() .
.
![]()
ЗАКЛЮЧЕНИЕ
Развитие современного общества характеризуется повышением технического уровня, усложнением организационной структуры производства, управления войсками, углублением общественного разделения труда, предъявлением высоких требований к методам планирования хозяйственного и военного руководства. В этих условиях только научный подход к руководству хозяйственной жизнью общества позволит обеспечить высокие темпы развития народного хозяйства. Научного подхода требует и решение тактических и стратегических задач, руководство военными операциями.
В настоящее время новейшие достижения математики и современной вычислительной техники находят все более широкое применение как в экономических исследованиях и планировании, так и в решении военных тактических задач. Этому способствует развитие таких разделов математики как математическое программирование, теория игр, теория массового обслуживания, а также бурное развитие быстродействующей электронно-вычислительной техники. Уже накоплен большой опыт постановки и решения экономических и тактических задач с помощью математических методов. Особенно успешно развиваются методы оптимального управления. Ярким примером применения современных математических методов является война Америки с Ираком и «Буря в пустыне». Там быстро развивается экономика и производство, где широко используются математические методы.
ЛИТЕРАТУРА
1. Тихонов А. Н., Костомаров Л. П. Вводные лекции по прикладной математике. М., Наука, 1984.
2. Кудрявцев Е. Н. Исследования операций в задачах, алгоритмах и программах. М., Наука, 1982.
3. Кузнецов Ю. Н., Кузубов В. И., Волощеноко А. В. Математическое программирование. М., Высшая школа, 1980.
4. Ильин В. А., Позняк Э. Г. Основы математического анализа. М., Наука, 1979.