Реферат: Загрезнения окружающей сруды
Обозначая через P численность популяции (в экологии часто используется обозначение N ), а время — t , модель сводится к дифференциальному уравнению:
![]()
где параметр r характеризует скорость роста (размножения), а K — ёмкость среды (то есть, максимально возможную численность популяции). Исходя из названия коэффициентов, в экологии часто различают две стратегии поведения видов:
- r -стратегия предполагает бурное размножение и короткую продолжительность жизни особей
- а K -стратегия — низкий темп размножения и долгую жизнь.
Точным решением уравнения (где P 0 — начальная численность популяции) является логистическая функция, S-образная кривая, (логистическая кривая):
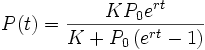
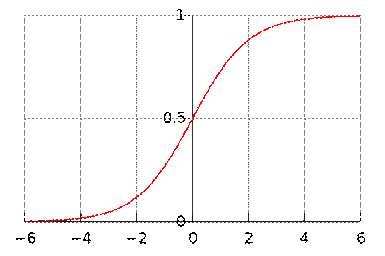
Логистическая кривая для K =1 и P 0 =0,5
где
![]()
Ясно, что в ситуации «достаточного объёма ресурсов», то есть пока P(t) много меньше K, логистическая функция поначалу растёт приблизительно экспоненциально:
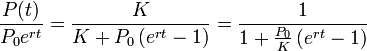
Аналогично, при «исчерпании ресурсов» (t → ∞) разность K − P(t) экспоненциально убывает с таким же показателем.
Почему Ферхюльст назвал уравнение логистическим, остается неизвестным. В 1924 году Раймонд Перл применил уравнение для описания автокаталитических реакций.
Автокатализ — катализ химической реакции одним из её продуктов или исходных веществ. Одним из наиболее широко известных примеров автокатализа является окисление щавелевой кислоты перманганатом калия:
2MnO4− + 5C2O42− + 16H+ = 2Mn2+ + 10CO2 + 8H2O
Катализатором этой реакции являются ионы Mn2+. При комнатной температуре эта реакция вначале протекает медленно, но по мере накопления в растворе продукта-катализатора, она ускоряется.
Дискретным аналогом логистического уравнения является логистическое отображение .
Логистическое отображение (также известное, как квадратичное отображение или отображение Фейгенбаума) — полиномиальное отображение, хрестоматийно упоминаемое в качестве типичного примера того, как сложное, хаотическое поведение может возникать из очень простых нелинейных уравнений. Отображение является дискретным аналогом непрерывного логистического уравнения Ферхюльста, отражая тот факт, что прирост популяции происходит в дискретные моменты времени.
Математическая формулировка отображения
![]()
где:
- x n принимает значения от 0 до 1 и отражает численность популяции в -ом году, а обозначает начальную численность (в год номер 0)
- r — положительный параметр, характеризующий скорость размножения (роста) популяции.
Иногда данная формулировка называется отображением Ферхюльста (или Ферхюльста-Пирла ), а логистическим отображением называется другая, но эквивалентная по свойствам формула
![]()
Это нелинейное отображение описывает два эффекта:
- размножение популяции, со скоростью, пропорциональной ее численности в момент, когда численность мала.
- конкуренцию (смертность при высокой плотности) за жизненные ресурсы, при которой скорость размножения падает из-за ограничения на «максимальную емкость» среды, в которой обитает популяция.
Одним из недостатков использования отображения в качестве демографической модели является тот факт, что при некоторых начальных значениях и величинах параметров отображение дает отрицательные значения численности популяции. Подобного недостатка лишена дискретная модель Рикера, которая также демонстрирует хаотическое поведение.
- ОБЬЕСНИТЕ ЭКОЛОГИЧЕСКИЙ СМЫСЛ ПРАВИЛА 1%
Проблема стабильности экосистем
- Что понимается под устойчивостью экосистемы?
- Объясните экологический смысл правила 1%.