Реферат: Зоны Френеля

Введение………………………………………………………………….…3

Принцип Гюйгенса - Френеля, зоны Френеля…………………………..4

Дифракция радиоволн на полуплоскости……………………………….8

Заключение……………………………………………………………….12

Литература………………………………………………………………..13

Введение

Необходимо отметить, что при распространении радиоволн в свободном пространстве различные его области не одинаково влияют на формирование электромагнитного поля в удаленной от излучателя точке приема. При этом всегда можно выделить некоторую область пространства, в которой распространяется основная часть передаваемой в заданном направлении энергии электромагнитных волн. Ее размеры и конфигурацию определяют исходя из известного из курса физики принципа Гюйгенса-Френеля.

Принцип Гюйгенса - Френеля, зоны Френеля.

Согласно принципу Гюйгенса, каждая точка фронта распространяющейся волны является источником новой сферической волны. При этом, если известно положение фронта волны S(t) в некоторый момент времени " t " (см. рис.1) и скорость волны " ", то положение фронта в последующий момент времени (t + ) можно определить поверхностью S(t+ ), огибающей все вторичные волны. Принцип Гюйгенса является чисто геометрическим и не указывает способа расчета амплитуды волны, огибающей вторичные волны. Поэтому, развивая указанный принцип, Френель предложил идею о когерентности вторичных волн и их интерференции, что позволяет определять полное поле в любой точке пространства как сумму элементарных волн, излучаемых "элементами Гюйгенса". Объединенные идеи Гюйгенса и Френеля известны в современной физике и электродинамике в качестве "Принципа Гюйгенса - Френеля".

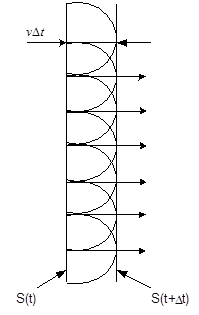
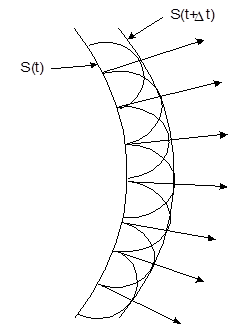
Рис. 1

Использование данного принципа позволяет достаточно просто определить размеры и форму области пространства распространения прямой электромагнитной волны.

Из теории электромагнитного поля известно, что каждый элемент фронта волны (элемент Гюйгенса), созданный каким-либо первичным источником, является вторичным источником сферической волны с характеристикой направленности в виде кардиоиды.

Математически характеристика направленности указанного элемента описывается функцией .

Если источник электромагнитного поля находится в некоторой точке А (рис. 2а), то полное поле в точке приема В можно определить, опираясь на вышеизложенное, воспользовавшись формулой Кирхгофа:

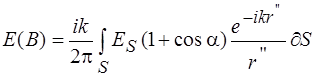, (1)

где - величина поля на элементе Гюйгенса, создаваемая первичным источником А;

r^’’ - расстояние от элемента Гюйгенса до точки приема; .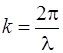

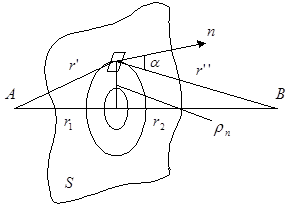
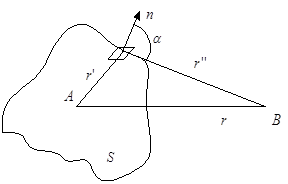
а) б)

Рис. 2

С учетом того, что:

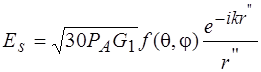,полное поле в точке В будет равно

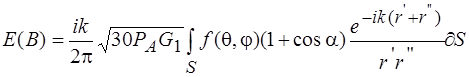. (2)

Поскольку форма поверхности не имеет значения, возьмем в качестве этой поверхности плоскость, расположенную на расстояниях r₁ и r₂ (r₁ + r₂ =r) от точек А и В перпендикулярно траектории прямой волны (см. рис. 2б). При этом фазы элементарных волн будут определяться соотношением = k(r' + r''), а для центральной элементарной волны = kr = k(r₁ + r₂ ).

Для упрощения анализа характера и степени вторичных элементарных источников электромагнитных волн, расположенных на поверхности S, на результирующее поле в точке В, разделим всю поверхность S на зоны Френеля.

Зона Френеля - это часть поверхности фронта электромагнитной волны, охватывающая вторичные источники, элементарные волны которых в точке В расходятся по фазе не более чем на 180⁰ , при этом соседние зоны Френеля создают в точке В противофазные поля.

Математически размер зоны определяется выражением:

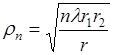(3)

Если перемещать воображаемую поверхность S вдоль линии АВ, то окружности радиуса опишут поверхности эллипсоидов вращения.

Области пространства между двумя соседними эллипсоидами вращения являются пространственными зонами Френеля (см. рисунок 3).

--> ЧИТАТЬ ПОЛНОСТЬЮ <--