Шпаргалка: Ответы на экзаменационные вопросы по теоретической механике
Решение первой задачи.
 |  |
????? ????? ????? ???????? ???????????? ????? ? ????,
А так же её равнодействующая и масса m.
Из дифференциального уравнения движения материальной точки в
 |  |
?????????? ??????? ????????? ???????, ???:
 |
?????????? ???????? ?????? ?????? ??? ????????? ?????, ????? ????? ???????????, ? ?? ????????? ?????????? ???????? ?????????? ????? ??????????? ?? ????? ????. ? ???? ??????:
 |
Пример.
![]()
Груз весом Р поднимается вертикально вверх по закону
Определить натяжение тросса.
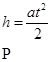 | 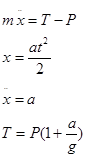 |
![]()
![]()
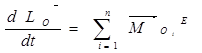 |
2)???????: ??????????? ?? ??????? ?? ????????????? ??????? ???????????? ??????? ???????????? ???????????? ?????? ????? ???????? ??????? ???? ??????? ???, ??????????? ?? ??????? ???????????? ???? ?? ??????.
5.1)Решение I-й задачи динамики. Пример.
2)Теорема об изменении количества движения точки и система в дифф.и конечной формах.
1)Решение первой задачи.
 | 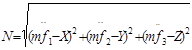 |
????? ????? ????? ???????? ???????????? ????? ? ????,
А так же её равнодействующая и масса m.
Из дифференциального уравнения движения материальной точки в
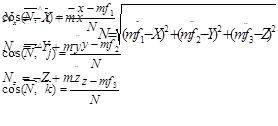 |
?????????? ??????? ????????? ???????, ???:
?????????? ???????? ?????? ?????? ??? ????????? ?????, ????? ????? ???????????, ? ?? ????????? ?????????? ???????? ?????????? ????? ??????????? ?? ????? ????. ? ???? ??????:
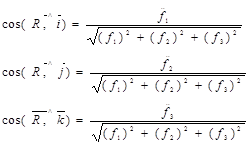 | 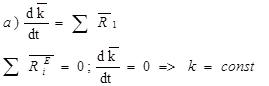 |
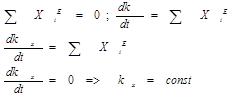 |
Пример.
![]()
Груз весом Р поднимается вертикально вверх по закону
Определить натяжение тросса.
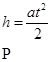 | 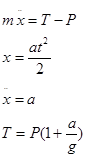 |
![]()
![]()
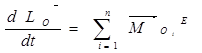 |
2)???????: ??????????? ?? ??????? ?? ????????????? ??????? ???????????? ??????? ???????????? ???????????? ?????? ????? ???????? ??????? ???? ??????? ???, ??????????? ?? ??????? ???????????? ???? ?? ??????.
2)З-н сохранения количества движения:
Если геометрическая сумма всех внешних сил, приложенных к механической системе = 0, то её вектор количества движения постоянен. Воспользуемся дифф.формой теоремы об изменении количества движения механической системы.
.б) Если алгебраическая сумма проекций на какую либо ось всех действующих сил системы = 0, то проекция её вектора количества движения на эту ось есть величена постоянная.
6.1)Решение II-й задачи динамики. Постоянные интегрирования и их определения по начальным условиям. Пример.
2)Кинетический момент механической системы относительно центра и оси. Кинетический момент твёрдого тела вращающегося относительно оси.
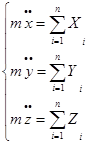
1)Для решения этой задачи целесообразно воспользоваться дифф.ур-ми мат.точки в виде:
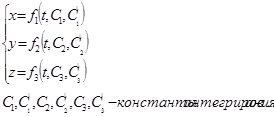
Поскольку действие силы известны, то => известны и правые части этих ур-й. Интегрирование их дважды по времени приводит их к 3-м ур-м содержащим 6 произвольным постонным:
![]()
Значе ния этих постоянных могут быть просто найдены с помощью нач.усл., т.е. если известно:
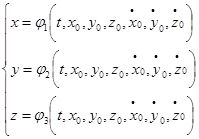
Подставив найденные значения в постоянные интегрирования в общее решение дифф-х ур-й получили закон движения точки:
Отсюда => , что мат.точка под действием одной и той же силы может совершать целый класс движений определённый начальными условиями.
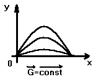 | 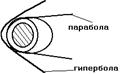 |
????????: ???????? ????????? ???.????? ??? ?????? ??????? ? ???????? ?????? 2-?? ???????.
Начальные условия позволяют учесть влияние на движение мат.точки сил дейсвовавших на неё до того момента, который принят за начальный.
2)Закон сохранения кинетического момента механической системы:
1)Если сумма моментов относительно данного центра всех внешних сил = 0, то кинетический момент механической системы сохраняет модуль и направление в пространстве