Шпаргалка: Ответы на экзаменационные вопросы по теоретической механике
Fистр
21.1) Кинетическая энергия материальной точки и механической системы. Вычисление кинетической энергии твердого тела в различных случаях его движения.
2)Закон сохранения количества движения механической системы. Примеры.
![]()
1)Кинетической энергией метер. т-ки называется величина равная половине произведения ее массы на квадрат скорости:
![]()
Кинетической энергией механической системы называется сумма кинетических энергий всех входящих в нее материальных точек:
2)
Если главный вектор всех действующих на систему внешних сил равен 0, то вектор количества движения системы есть величина постоянная.
Если алгебраическая сумма проекций на какую-нибудь ось всех действующих на механическую систему внешних сил равна 0, то проекция вектора количества движения на эту ось есть величина постоянная.
22.1)Элементарная работа силы, ее аналитическое выражение. Работа силы на конечном пути. Работа силы тяжести.
2)Главные оси и главные моменты инерции. Свойства главных осей и главных центральных осей инерции.
1)Элементарной работой силы F называется скалярное произведение: A=(F∆r), где ∆r вектор элементарного перемещения точки, приложения силы, произошедшего в результате действия силы.
![]()
Работа силы на конечном перемещении равна алгебраической сумме ее работ на отдельных элементарных участках:
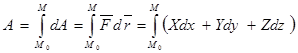
При движении тела по непрерывной траектории можно перейти к пределу при стремлении числа участков к бесконечности и получить:
2)Поскольку уравнение не содержит координат первой степени, то его центр совпадает с началом координат. Три оси симметрии эллипсоида инерции называются – главными осями инерции относительно точки 0, а момент инерции относительно осей – главным моментом инерции.
Если выбрать систему координат так, что бы оси совпадали с главными осями инерции механ. сист, то уравнение эллипса примет вид: J* x X2 * + J* y Y2 * + J* z Z2 * = 1
Каждой точке соотв. свой эллипс инерции и если он известен, то можно найти момент инерции относительно любой оси, проходящей через данную точку. Эллипсоид, соотв. центру масс тела называется центральным эллипсоидом инерции, а его оси симметрии главными центральными осями инерции.
Если известны главные центры моментов инерции, то можно построить центр эллипсоид. инерции, а отсюда следует определение: моментом инерции относительно любой оси, проходящей через центр масс системы.
23.1) Работа силы упругости и силы тяготения. Работа сил, приложенных к твёрдому телу, вращающемуся вокруг неподвижной оси.
2)Теорема об изменении кинетического момента механической системы по отношению к центру масс.
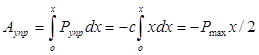 |
?????? ???? ?????????.
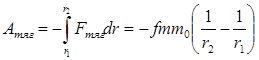 |
Работа силы тяготения.
Работа сил на конечном перемещении равна произведению главного момента внешних сил относительно оси вращения на конечное изменение угла поворота тела.
2)А) Относительно неподвижного центра Производная по времени от кинетического момента относительно неподвижного центра равна главному моменту всех внешних сил, действующих на систему относительно того же центра. Б) Относительно центра системы координат, движущимся поступательно вместе с центром масс. Производная по времени от кинетического момента механической системы, относительно центра системы координат, движущимся поступательно вместе с центром масс, равна главному моменту всех внешних сил, относительно центра масс.
24.1)??????? ?? ????????? ???????????? ??????? ??? ????? ? ???????????? ??????? ? ?????? ? ???????? ??????.
2)Потенциальная энергия мат точки и механ системы. Поверхность равного потенциала.
1)???????. ????????? ???????????? ??????? ????? ??????? ?? ????????? ??????????? = ????? ????? ??????? ? ?????????? ???, ??????????? ?? ??? ????? ??????? ?? ???? ???????????.
Конечная форма.
2) Потенциальная энергия системы в любом данном её положении = сумме работ сил потенциального поля, приложенных к её точкам на перемещении системы из данного положения в нулевое.
![]()
Пусть U=U(x ,y ,z)- силовая функция поля.
П=П(x, y, z)- потенциальная энергия точки.
Уравнение П( x, y, z) определяет некоторую поверхность в пространстве, которая называется поверхностью равного потенциала или эквипотенциальной поверхностью.
25.1)Закон сохранения механической энергии системы при действии на неё потенциальных сил.