Сочинение: Доказательство теоремы Ферма для n=4

Пусть:

N=P∙S; M=S²

Тогда:

K= С² +В² = 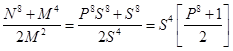(15)

Из уравнений (4), (5) и (15) следует:

A⁴ = N⁴ ∙ K=N⁴ · S⁴ ∙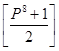 (16)

Отсюда следует:

A = N· S∙ (17)

Очевидно, что:

- дробное число.

То есть:

С² + В² ≠ R⁴ ; A⁴ ≠ N⁴ ∙R⁴

Следовательно, в соответствии с формулой (17) число А - дробное число.

Другими словами, определенные по формулам (11) и (12) значения чисел B и С удовлетворяют только уравнению (5) и не удовлетворяют предполагаемому равенству:

С² + В² = R⁴

Таким образом, великая теорема Ферма не имеет решения в целых положительных числах для показателя степени n=4.