Сочинение: Доказательство теоремы Ферма для n=4

Великая теорема Ферма формулируется следующим образом: диофантово уравнение:

Аⁿ + Вⁿ = Сⁿ (1)

где n - целое положительное число, большее двух, не имеет решения в целых положительных числах.

Суть Великой теоремы Ферма не изменится, если уравнение (1) запишем следующим образом:

Аⁿ = Сⁿ - Вⁿ (2)

Пусть показатель степени n=4. Тогда уравнение (2) запишется следующим образом:

А⁴ = С⁴ -В⁴ (3)

Уравнение (3) запишем в следующем виде:

А⁴ = (С² ) ² - (В^{2) 2} = (С² -В² ) ∙ (С² +В² ) (4)

Пусть: (С² -В² ) = N⁴ (5)

Уравнение (5) рассматриваем как параметрическое уравнение 4 - ой степени с параметром Nи переменными Bи С. Преобразуем уравнение (5):

N⁴ = (С -В) · (С +В) (6)

Для доказательства используем метод замены переменных. Обозначим:

C-B=M (7)

Из уравнения (7) имеем:

C=B+M (8)

Из уравнений (6), (7) и (8) имеем:

N⁴ =M∙ (B+M+B) =M∙ (2B+M) = 2B∙M+M² (9)

Из уравнения (9) имеем:

N⁴ - M² = 2B∙M (10)

Отсюда:

B=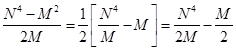 (11)

Из уравнений (8) и (11) имеем:

C= 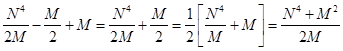(12)

Из уравнений (11) и (12) следует, что необходимым условием для того чтобы числа В и С были целыми, является делимость числа N⁴ на число M, т.е. число Mдолжно быть одним из сомножителей, входящих в состав сомножителей числа N⁴ .

Из уравнений (11) и (12) также следует, что необходимым условием для того чтобы числа В и С были целыми, является также одинаковая четность чисел Nи M: оба числа должны быть четными или оба нечетными.

Из уравнений (11) и (12) также следует:

С² +В² = 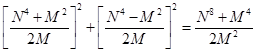(13)

Обозначим:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--