Сочинение: Гипотеза Биля

U= 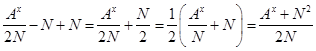/14/

Из уравнений /5/, /6/, /13/ и /14/ имеем:

В = /15/

С = /16/

Из уравнений /13/, /14/, /15/ и /16/ следует: если допустить, что числа V и U могут быть дробными числами, то они могут быть только рациональными дробными числами. Однако никакое рациональное дробное число, возведенное в квадрат, не равно целому числу, тем более:

V2 ≠ (abc…) y; U2 ≠ (def…) z

Поэтому из уравнений /15/ и /16/ следует: необходимым условием для того чтобы числа В и С были целыми, числа V и U должны быть также целыми.

Из уравнений /13/ и /14/ в виде:

V= и U=

Следует, что число N должно быть делителем числа Аx, т.е. входить как множитель в число Аx. Если число N является составным числом, т.е. является произведением нескольких простых чисел, то оно должно быть произведением множителей, входящих в состав числа Аx.

Из уравнений /13/ и /14/ в виде:

V= иU=

также следует, что поскольку знаменатели дробей содержат цифру 2, числители должны делиться на 2. Это условие выполняется только в том случае, если числа А и N оба четные или оба нечетные.

Из уравнения /13/ следует, что поскольку число V, исходя из выше принятого условия, должно быть целым положительным числом, должны выполняться условия:

Аx-N2 > 0; или: N2 < Аxи: Аx- N2 >2N.

Установим cоотношения между числами В и С. Разделив уравнение /15/ на уравнение /16/, получим:

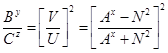/17/

Отсюда:

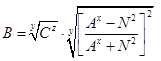/18/

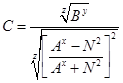/19/

Алгебраическое выражение:

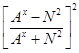<1 - дробное рациональное число.

Алгебраические выражения:

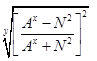<1 - при y>2 - дробное число. /20/

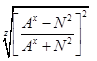<1 - при z>2 - дробное число. /21/

Из анализа алгебраических выражений /20/ и /21/ следует, что из одного и того же дробного числа извлекаются корни разных степеней y и z, при этом показатели степени y и zпо условию гипотезы Биля взаимно простые числа. Очевидно, что после извлечения корней, по крайней мере, одно из чисел будет иррациональным дробным числом.

Следовательно, одно из чисел B или C или оба - дробные числа.

Таким образом, гипотеза Биля не имеет решения в целых положительных числах.