Статья: Бинарные жидкие системы

Общее давление насыщенного пара над раствором будет равно (закон Дальтона):

. (8.8)

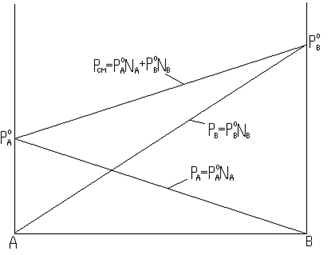
Зависимость парциального и общего давления паров смеси от ее состава показана на рис. 8.3, где на оси ординат отложено давление насыщенных паров, а на оси абсцисс – состав раствора в мольных долях. При этом по оси абсцисс содержание одного вещества (А) убывает слева направо от 1,0 до 0 мольных долей, а содержание второго компонента (В) одновременно в том же направлении увеличивается от 0 до 1,0. При каждом определенном составе общее давление насыщенного пара равняется сумме парциальных давлений. Общее давление смеси изменяется от давления насыщенного пара одной индивидуальной жидкости до давления насыщенного пара второй чистой жидкости.

Законы Рауля и Дальтона часто используются для оценки пожарной опасности смесей жидкостей.

Состав смеси, мольные доли

Рис. 8.3 Диаграмма состав раствора – давление насыщенного пара

Обычно состав паровой фазы не совпадает с составом жидкой фазы и паровая фаза обогащена более летучим компонентом. Это различие можно изобразить и графически (график имеет вид аналогичный графику на рис. 8.4, только на оси ординат взята не температура а давление).

В диаграммах, представляющих зависимость температур кипения от состава (диаграмма состав-температура кипения рис. 8.4), обычно принято строить две кривые, одна из которых связывает эти температуры с составом жидкой фазы, а другая с составом пара. Нижняя кривая относится к составам жидкости (кривая жидкости), а верхняя – к составам пара (кривая пара).

Поле, заключенное между двумя кривыми, соответствует двухфазной системе. Любая точка, находящаяся в этом поле, отвечает равновесию двух фаз – раствора и насыщенного пара. Состав равновесных фаз определяется координатами точек, лежащих на пересечении изотермы, проходящей через кривые, и данную точку.

При температуре t1 (при данном давлении) будет кипеть жидкий раствор состава х1 (точка а1 на кривой жидкости), пар, равновесный с этим раствором, обладает составом х2 (точка b1 на кривой пара).

Т.е. жидкости состава x1 будет соответствовать пар состава х2.

Исходя из выражений: , , , ,

взаимосвязь между составом жидкой и паровой фаз может быть выражена соотношением:

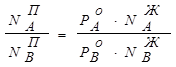. (8.9)

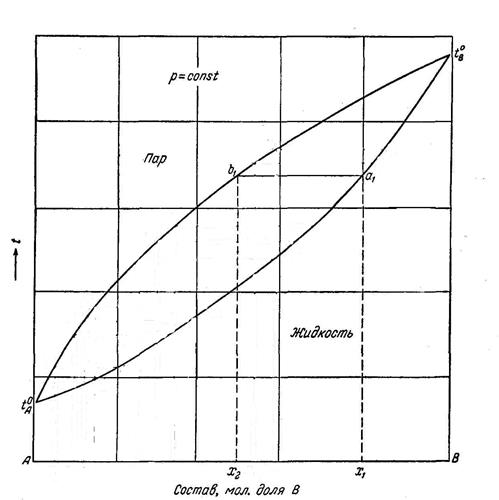
Рис. 8.4. Диаграмма состав-температура кипения двойных смесей.

Реальное давление насыщенного пара индивидуальной жидкости при данной температуре есть характерная величина. Практически нет жидкостей, которые бы обладали одинаковыми значениями давления насыщенного пара при одной и той же температуре. Поэтому всегда больше или меньше . Если >, то >, т.е. состав паровой фазы обогащен компонентом А. Изучая растворы, Д.П. Коновалов (1881г.) сделал обобщение, получившее название первого закона Коновалова.

В двойной системе пар, по сравнению с находящейся с ним в равновесии жидкостью, относительно богаче тем из компонентов, прибавление которого к системе повышает общее давление пара, т.е. понижает температуру кипения смеси при данном давлении.

Первый закон Коновалова является теоретической основой для разделения жидких растворов на исходные компоненты путем фракционной перегонки. Например, система, характеризуемая точкой К, состоит из двух равновесных фаз, состав которых определяется точками a и b: точка а характеризует состав насыщенного пара, точка b - состав раствора.

По графику можно провести сопоставления составов паровых и жидких фаз для любой точки, заключенной в плоскости между кривыми.

Реальные растворы. Закон Рауля не выполняется для реальных растворов. Отклонение от закона Рауля существует двух типов:

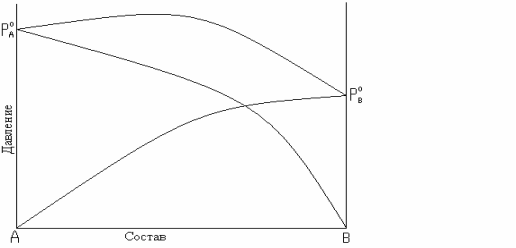
парциальное давление растворов больше давлений или летучести паров идеальных растворов. Общее давление пара больше аддитивной величины. Такие отклонения называются положительными, например, для смесей (рис. 8.5 а, б) CH3COCH3-C2H5OH, CH3COCH3-CS2, C6H6- CH3COCH3, H2O-CH3OH, C2H5OH-CH3OCH3, CCl4-C6H6 и др.;

а

б

Рис. 8.5. Зависимость общего и парциальных давлений пара от состава:

а – для смесей с положительным отклонением от закона Рауля;

б – для смесей с отрицательным отклонением от закона Рауля.