Статья: Физико-математическое моделирование и анализ эффекта квантования магнитного потока

В рамках гипотезы монополя Дирака установлен магнитный заряд электрона, тождественно равный кванту магнитного потока, наблюдаемого в условиях сверхпроводимости. На этой основе сделан вывод о том, что все микрочастицы обладают в совокупности как электрическим, так и магнитным зарядами, которые в изоляции друг от друга в Природе не существуют, при этом спин микрочастиц является результатом электромагнитного взаимодействия этих собственных зарядов.

В физике известен эффект квантования магнитного потока [1] - макроскопическое квантовое явление, состоящее в том, что магнитный поток через кольцо из сверхпроводника с электрическим током может принимать лишь строго дискретные значения, кратные минимальной величине 2,07.10–15 Вб (Вебер) - кванту магнитного потока. Указанный физический феномен был предсказан в 1948 году Ф. Лондоном [2], который теоретически получил для кванта магнитного потока соотношение , где h - постоянная Планка, е - заряд электрона. Однако позднее (1961г.) экспериментально установлено [3, 4] вдвое меньшее значение этого кванта: , что общепринято считать объективным непосредственным подтверждением основной идеи созданной к тому времени микроскопической теории сверхпроводимости [1].

Согласно этой теории, сверхпроводящее состояние кристалла обусловлено фазовой пространственно-временной когерентностью носителей тока в виде квазичастиц Бозе-конденсата, образованных электрон-фононным взаимодействием пространственно разнесенных пар электронов проводимости (Купера эффект [1]), обладающих нулевым спином и зарядом, равным удвоенному заряду электрона. Именно пространственное парное взаимодействие электронов проводимости (куперовских пар 10-6 м) физически реализует явление сверхпроводимости, поскольку в процессе электропроводности «столкновения» отдельного электрона с ионами кристаллической решетки не способны изменить суммарного механического импульса его электронной пары (ее центра масс).

Анализ эффекта квантования магнитного потока начнем с исследования базовой в теории электричества теоремы Гаусса [5], описывающую электрическую поляризацию материальной среды, представленной как в дифференциальной , так и в интегральной формах. Здесь - поле вектора электрической индукции (смещения), обусловленное откликом среды при воздействии на нее поля вектора - электрической напряженности; - абсолютная электрическая проницаемость, - объемная плотность стороннего электрического заряда. Однако следует иметь в виду, что равенство нулю стороннего заряда, соответственно, его электрического потока отнюдь не означает отсутствие электрического поля в этой области пространства, поскольку электрические заряды бывают положительными и отрицательными, и указанное поле может создаваться электронейтральными источниками, например, электрическими диполями, посредством которых реализуется процесс поляризации. Такое свойство электростатического поля качественно отличает его от ньютоновского поля тяготения, там источники этого поля – гравитирующие массы имеют лишь один знак.

Итак, уравнение описывает поляризацию локально электронейтральной () среды, откуда с учетом тождества векторного анализа получим фундаментальное следствие теоремы Гаусса: , где - векторный электрический потенциал. В интегральной форме это соотношение описывает функциональную связь циркуляции поля вектора по замкнутому контуру с потоком вектора электрической индукции через опирающуюся на этот контур поверхность , на которой, согласно физике явления поляризации, индуцирован порождающий это поле электрический поляризационный заряд:

, (1)

n - целые числа. Таким образом, имеем тождественную симметрию размерностей потока вектора поля электрической индукции (смещения) и электрического заряда: электрический поток - - [] - электрический заряд. При этом квант электрического заряда - электрон может быть тождественно представлен квантом электрического потока: .

Полностью следуя логике вышеприведенных рассуждений при анализе связи квантов электрического заряда и потока его поля, перейдем теперь собственно к анализу эффекта квантования магнитного потока. Для этого воспользуемся соотношением, описывающим результат магнитной поляризации материальной среды , которое часто не вполне оправдано называют теоремой Гаусса для магнитного поля, в виде его прямого математического следствия: , где - векторный магнитный потенциал, а - вектор поля магнитной индукции. Интегральная форма данного соотношения описывает функциональную связь циркуляции вектора по контуру с потоком вектора индукции через опирающуюся на этот контур поверхность , на которой, согласно нашему предположению, индуцирован порождающий это магнитное поле гипотетический магнитный поляризационный заряд:

. (2)

Таким образом, имеем тождественную симметрию размерностей вектора поля магнитной индукции и поляризационного магнитного заряда (если таковой существует): магнитный поток - - [] - магнитный заряд. А поскольку величина кванта магнитного потока однозначно установлена в экспериментах [3, 4], то, согласно соотношению (2), квант магнитного заряда тождественно определится квантом магнитного потока: . В этой связи приходится констатировать, что положительные результаты экспериментов по наблюдению кванта магнитного потока в работах [3, 4] безусловно, являются физическим открытием магнитного заряда и величины его кванта.

Кстати, именно этот вопрос является центральным в настоящем исследовании. Главная здесь задача – это независимым путем аналитически доказать объективность неразрывной связи и равноправного единства сущностное разных зарядов в виде соотношения «», полученного нами при анализе экспериментов по наблюдению эффекта квантования магнитного потока [3, 4].

Напомним, что гипотеза о возможности существования магнитного монополя - частицы, обладающей положительным или отрицательным магнитным зарядом, аналогичным электрическому заряду, была высказана П.А.М. Дираком (1931г.) с целью концептуального обоснования симметричной квантовой электродинамики, именно эту частицу и называют монополем Дирака [1, 6]. Однако монополь Дирака не только экспериментально неуловим, но и теоретические построения по этому вопросу не позволяют даже по порядку величины определить еще один важный параметр магнитного заряда – массу его носителя. Справедливости ради отметим, что и масса электрона также не устанавливается настоящими теориями, являясь экспериментальным фактом. И все же каких-либо физических законов и очевидных логических возражений против идеи существования магнитных монополей нет, а потому в течение уже многих десятилетий интерес к этой физически актуальной проблеме не ослабевает.

Вот и мы представим себе, что наряду с реально наблюдаемыми положительными и отрицательными электрическими зарядами, порождающими в пространстве электрическое кулоновское поле [5], в Природе, возможно, существуют и свободные магнитные заряды - источники магнитного поля, отвечающего закону Кулона взаимодействия неподвижных точечных зарядов. Конечно, здесь надо иметь в виду, что многолетние упорные поиски свободных магнитных зарядов остаются безуспешными, однако закон Кулона магнитного взаимодействия в эксперименте действительно наблюдается, но только для магнитных полюсов на концах длинных намагниченных спиц.

Для физико-математического моделирования эффекта квантования магнитного потока рассмотрим взаимодействие постоянного во времени электрического тока с магнитным статическим полем, созданным предполагаемыми поляризационными магнитными зарядами. Конкретно, проведем анализ поведения элементарного электрического заряда - электрона «» при его движении с постоянной по модулю скоростью ортогонально силовым линиям однородного статического поля магнитной индукции . Согласно теории электричества [5], взаимодействие движущегося электрического заряда с магнитным полем реализуется посредством магнитной составляющей силы Лоренца , сообщающей частице центростремительное ускорение ( - масса электрона), приводящее к движению заряда по окружности радиуса . Тогда момент импульса электрона запишется в виде . Однако, здесь важно то, что согласно принципам корпускулярно-волнового дуализма материи [7] момент импульса микрочастицы квантуется, когда , где - целое число длин волн де Бройля частицы , укладывающихся на траектории ее орбиты, - модифицированная постоянная Планка.

А вот теперь будем считать, что источником магнитного поля являются гипотетические поляризационные магнитные заряды со свойствами, идентичными реальным электрическим зарядам . Для анализа воспользуемся результатами уже проведенной выше процедуры получения соотношения (2) функциональной связи магнитного заряда и потока его магнитного поля:

.

Отсюда находим нормальную составляющую вектора магнитной индукции , где - площадь орбиты электрона. Итак, окончательно момент импульса частицы запишется как . В итоге получаем тождественные друг другу квантованные величины магнитного заряда и потока его поля: , при этом квант магнитного заряда представится как , где в произведение минимальных величин электрического и магнитного зарядов входит постоянная Планка. Как видим, соотношение описывает неразрывную связь сущностно разных зарядов, равную с коэффициентом модулю кванта собственного углового момента микрочастиц, отвечающего, как известно [1, 7], спину электрона .

Таким образом, результаты физико-математического моделирования эффекта квантования магнитного потока действительно совпадают с итогами экспериментов, описанными в работах [3, 4]. Но тогда выходит, что широко известное аналитическое выражение для кванта магнитного потока , где якобы в знаменателе фигурирует величина заряда электронной пары - физической сути явления сверхпроводимости, на поверку представляет собой отношение значений корпускулярных электромагнитных характеристик только одного электрона: с коэффициентом спина этой микрочастицы к ее электрическому заряду.

Кстати, по результатам анализа эффекта квантования магнитного потока, приходим, на наш взгляд, к вполне разумному выводу о том, что непосредственным источником магнитного поля при электропроводности являются, как и должно быть физически, именно и только спины носителей тока, а не некий мифический релятивизм. Как представляется, электрический ток в виде упорядоченного дрейфового движения, например, электронов проводимости за счет нулевой в среднем их относительной скорости в направлении тока создает условия для взаимодействия магнитных моментов этих зарядов, то есть возникающее при этом упорядочение спинов проявляет себя на макроуровне в виде

магнитного поля тока. В процессе сверхпроводимости величина флуктуаций силы тока, соответственно, шумовой фон магнитного поля настолько малы, что дают возможность наблюдать еще более тонкое явление - эффект квантования магнитного потока. В итоге можно считать, что, наконец-то, удалось вскрыть физический механизм магнитного поля тока, напрямую коррелирующий с традиционными представлениями о спиновом механизме истинного магнетизма.

Итак, сравнительно простые рассуждения с привлечением базовой идеи квантовой (волновой) механики - корпускулярно-волнового дуализма материи позволили получить ряд действительно фундаментальных результатов, которые со всей определенностью ставят вопрос о необходимости серьезной концептуальной модернизации основ классической электродинамики.

Однако сейчас перед нами стоит не столь глобальная, но не менее важная задача: хотелось бы понять, почему не удается экспериментально обнаружить свободных магнитных монополей, да и вообще, возможны ли они в Природе? Для этого определим отношение сил Кулона взаимодействия пар неподвижных элементарных электрических «» и магнитных «» зарядов в вакууме:

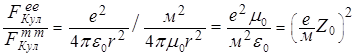, (3)

где - импеданс пространства физического вакуума. Как видим, результат, несомненно, физически интересен, так как обе силы Кулона связаны друг с другом фундаментальными константами: , причем сила кулоновского взаимодействия магнитных зарядов больше аналогичной электрической силы на три порядка: .

В качестве примера сделаем оценку энергетических затрат по реализации свободного заряда на примере процесса ионизации атома - характерной стационарной электронейтральной структуры, удовлетворяющей теореме Ирншоу [5]. Согласно теории Н. Бора атома водорода [7], формула минимальной энергии ионизации такого атома имеет вид и численно равна . Тогда для магнитной атомной структуры с учетом соотношений (3) получим боровскую формулу энергии ионизации магнитного атома: . При числовой оценке энергии учтем замечание выше о заряде в соотношении для кванта магнитного потока и возьмем массу кванта магнетизма , равную массе электрона . В итоге имеем . Как видим, разделение на части магнитонейтральной структуры в виде атома потребует энергии на 6 порядков больше, в сравнение с аналогичной процедурой над подобной электронейтральной структурой.

И хотя атомы, их ядра и всякого рода элементарные частицы обладают магнитными моментами, однако многочисленные эксперименты по ионизации атомов, изучение ядерных реакций, анализ взаимодействия и распада элементарных частиц в отношении наблюдения свободных магнитных зарядов оказались безуспешными. Причем при энергиях больше эВ получают множество различного сорта элементарных частиц с кратным заряду электрона электрическими зарядами и кратным постоянной Планка магнитными моментами, но и здесь магнитных монополей никто пока не наблюдал.

Согласно выводам нашего анализа, в любых физических процессах на современных установках, в том числе и на суперколлайдере (БАК) с энергией эВ, создать магнитный монополь энергетически невозможно. Одна надежда - это потоки частиц космических излучений, где энергия разного рода событий во Вселенной, образно говоря, беспредельна. Но и здесь многолетние технически сложные поиски монополя Дирака остаются безуспешными.

Таким образом, имеем парадоксальную ситуацию: с одной стороны, прямое наблюдение изолированных магнитных монополей невозможно энергетически, а, скорее всего, в таком виде в Природе их просто нет, но с другой стороны, установлено равноправное сосуществование электрических и магнитных зарядов, произведение квантов которых равно с точностью до кванту собственного момента микрочастиц [7]. Такая взаимозависимость физических характеристик разнородных и зарядов явно указывает на реальность силового взаимодействия между ними, а это уже повод серьезно задуматься: а вообще, могут ли существовать эти заряды по отдельности друг от друга? Конечно, здесь вполне естественны определенные сомнения в правомерности столь странной трактовки полученных результатов, а потому необходима весомая дополнительная аргументация.

С этой целью аналогично электрическому закону Кулона чисто формально запишем закон Кулона взаимодействия электрического и магнитного зарядов, который для их квантов «» представится равенством соотношений:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--