Статья: Фундаментальный предел скорости гравитации и его измерение
Согласно современной физической картине мира, наша Вселенная устроена достаточно просто и может быть описана с помощью всего лишь нескольких фундаментальных констант. Фундаментальная константа - это численная характеристика фундаментального закона природы. Она определяет физические свойства того явления, которое входит в рассматриваемый закон. Скорость света, постоянная Планка и гравитационная постоянная - вот главные фундаментальные физические константы теоретической физики, из которых могут быть построены планковские единицы массы (10-5 г), длины (10-33 см) и времени (10-43 с). Свет - это проявление одного из двух наиболее доступных восприятию человека классических фундаментальных полей - электромагнитного. Второе классическое поле - гравитационное - также легко обнаруживается всякий раз, когда мы наблюдаем падение какого-либо предмета на Землю. Фундаментальная константа скорости света связана с распространением электромагнитного поля. Оказывается, что и гравитационное поле может распространяться, предельная скорость его распространения называется скоростью гравитации. Гравитация, вообще говоря, физически никак не связана с электромагнитным полем. Поэтому скорость гравитации могла бы быть в принципе отличной от скорости света.
В теории Ньютона она равна бесконечности, и гравитационное поле распространяется мгновенно от источника, как бы далеко мы от него ни находились. С другой стороны, теория относительности Эйнштейна постулирует, что скорость гравитации должна быть равна скорости света. Так ли это на самом деле? На данный вопрос мы и попытаемся ответить.
Скорость света
В настоящее время мы хорошо знаем, что свет имеет электромагнитную природу. Это предсказание было сделано величайшим физиком XIX в. создателем теории электромагнитного поля Джеймсом Клерком Максвеллом (1831 - 1879). Согласно его теории, видимый свет представляет собой плоскую электромагнитную волну, распространяющуюся в пустом пространстве (вакууме) с постоянной скоростью около 300 000 км/с. Постоянство этой скорости и её независимость от движения источника света и наблюдателя были проверены в множестве экспериментов, как в лаборатории, так и при наблюдении различных астрономических объектов. Скорость света огромна, и неудивительно, что долгое время она считалась бесконечной.
Первым, кто зародил сомнение в бесконечности скорости света, был Галилео Галилей (1564 - 1642) - знаменитый итальянский физик, живший на два столетия раньше Максвелла. Галилей предложил опыт для измерения скорости света, результат которого оказался отрицательным, так как точность измерительных инструментов, доступных Галилею (главным образом, часов), была совершенно недостаточной, чтобы измерять промежутки времени, за которые свет проходит расстояние между двумя точками на поверхности Земли. Результат эксперимента Галилея убедил подавляющее большинство физиков в неоспоримости того факта, что скорость света бесконечна.
Тем не менее гипотеза Галилея находила и сторонников, которых не смутил отрицательный результат его опыта. Одним из таких исследователей был Олаф Ремер (1644 - 1710) - датский астроном, живший и работавший в Париже. Он систематически наблюдал один из галилеевых спутников Юпитера - Ио - и обнаружил, что его движение не подчиняется в полной мере закону всемирного тяготения Ньютона. Отклонения носили периодический характер с периодом в один год. Ремер, безоговорочно доверяя теории Ньютона, выдвинул гипотезу, что наблюдаемое возмущение в движении Ио обусловлено конечной скоростью света, используемого для его наблюдений. Солнечный свет, отражаемый Ио, требует больше времени, чтобы достичь Земли, когда она движется по своей орбите от Юпитера, и меньше, когда ее движение происходит в сторону планеты-гиганта. Ремер получил скорость света, равную 210 000 км/с. Однако его результат не был поддержан ведущими французскими физиками того времени - Дж. Кассини (1625 - 1712) и Р. Декартом (1596-1650). Лишь много позднее, в 1725 г., Джэймс Брадлей (1693-1762) использовал наблюдения эффекта аберрации света и безоговорочно доказал, что свет распространяется с конечной скоростью.
В начале ХХ столетия Альберт Эйнштейн (1879-1955) создал специальную теорию относительности. Ее главный постулат гласит, что скорость света в вакууме постоянна, не зависит от выбора системы координат и движения наблюдателя. Этот постулат подтвержден результатами многочисленных экспериментов и в настоящее время не вызывает сомнений. Эйнштейн предположил также, что скорость света является предельной скоростью движения физических тел и распространения любых физических взаимодействий.
Скорость гравитации
Возвращаясь к гравитационному полю, мы вправе задать вопрос о предельной скорости его распространения. Соответствует ли она постулату специальной теории относительности?
Представим себе, что Солнце внезапно исчезло из центра нашей Солнечной системы. Через какое время Земля почувствует его исчезновение? Для света вопрос решен, так как досконально известно, что свет распространяется с конечной скоростью и поэтому оптически исчезновение Солнца станет заметно только через 8 мин 20 с - ровно столько свету надо, чтобы преодолеть расстояние в одну астрономическую единицу, отделяющую нас от Солнца.
Общая теория относительности (ОТО) Эйнштейна предсказывает точно такое же время и для исчезновения гравитационного притяжения Солнца на орбите Земли. В этом случае Земля продолжит движение по своей орбите в течении еще 8 мин 20 с, а затем начнет двигаться по прямой линии, так как притяжения Солнца не будет. В отличие от теории относительности Ньютоновская теория дает диаметрально противоположный результат: с исчезновением Солнца Земля мгновенно почувствует его отсутствие. Но как доказать, что права теория относительности? Можем ли мы уже сейчас экспериментально надежно установить скорость распространения гравитационного взаимодействия?
Известно, что основные положения теории относительности были проверены большим количеством высокоточных измерений как внутри Солнечной системы, так и за ее пределами. Основные релятивистские эксперименты внутри Солнечной системы включают измерение аномального смещения перигелия Меркурия, отклонения лучей света и запаздывания радиоволн вследствие влияния гравитационного поля Солнца. В настоящее время точность этих экспериментов достигла рекордной величины - одной десятитысячной от величины измеряемого эффекта. Однако Солнце расположено недалеко от центра масс всей Солнечной системы, и изменения гравитационного поля, вызываемые небольшими долговременными колебаниями положения Солнца относительно этой точки, пренебрежимо малы. Поэтому релятивистские эффекты, порождаемые нестационарностью гравитационного поля Солнца, невозможно измерить. Скорость распространения гравитационного взаимодействия (скорость гравитации) можно измерить только в том случае, если гравитационное поле является переменным и эта переменность достаточно быстрая, чтобы возникли гравитационные релятивистские эффекты, доступные для современной измерительной техники, применяемой в астрономии. При этом возможны два метода один из которых основан на детектировании гравитационных волн и измерения скорости их распространения, а второй - на измерении деформации структуры силовых линий поля, также называемом аберрацией гравитации (по аналогии с аберрацией света).
Двойные пульсары и гравитационные волны
Быстропеременные гравитационные поля создаются, например, двойными пульсарами, состоящими из тесной пары: нейтронная звезда - нейтронная звезда или нейтронная звезда - черная дыра. Один из подобных объектов, PSR B1913+16, был открыт в 1974 г. американскими астрофизиками Расселом Халсом и Джозефом Тэйлором. Несколько лет непрерывных наблюдений показали, что орбитальный период этой системы непрерывно уменьшается. Ученые предположили, что такой эффект - следствие потери орбитальной энергии, уносимой гравитационными волнами, излучаемыми данным космическим объектом. Сравнение теоретических расчетов с экспериментальными результатами подтвердило первоначальное предположение и послужило косвенным указанием на существование гравитационных волн в полном соответствии с ОТО Эйнштейна. Излучение гравитационных волн порождает силу, тормозящую орбитальное движение пульсара и его компаньона (предположительно, нейтронной звезды), - силу реакции гравитационного излучения. Ее существование в общей теории относительности было теоретически доказано в работах Т. Дамура (Франция), Г. Шэфера (Германия), Л.П. Грищука и С.М. Копейкина (Россия) и подтверждено экспериментально Дж. Тэйлором и его сотрудниками.
Но можно ли использовать наблюдения PSR B1913+16 для измерения скорости гравитационных волн? Вероятно, да, но это требует включения дополнительного параметра скорости гравитации в теоретические расчеты переменной силы реакции гравитационного излучения. Такие расчеты, из-за их неимоверной сложности, никогда не проводились, и мы не знаем точного вида формул, которые следовало бы использовать для определения скорости гравитации по наблюдениям двойного пульсара. Единственное четкое утверждение, которое можно сделать, заключается в том, что наблюдения двойного пульсара не противоречат предположению о том, что скорость гравитации равна скорости света. Именно этот постулат и был использован Дж. Тэйлором в его экспериментальной работе.
Развитие новых измерительных методов в радиоастрономии, в первую очередь радиоинтерферометрии со сверхдлинной базой, стимулировало наши исследования в области релятивистской астрометрии и небесной механики, и мы попытались подойти к вопросу об измерении скорости гравитации путем изучения аберрационных свойств гравитационного поля, используя наши новейшие теоретические разработки в области распространения электромагнитных сигналов через переменные гравитационные поля.
Эффект гравитационной линзы
Электромагнитные сигналы распространяются в пространстве-времени по наикратчайшему пути, который называется геодезической линией. В отсутствии гравитационного поля пространство-время плоское и геодезические линии - это прямые. Однако гравитационное поле изменяет структуру пространства-времени и искривляет его. Вследствие этого геодезические линии, по которым движется свет, тоже искривляются. Если источник гравитационного поля - массивное тело, то лучи света, распространяющиеся в поле данного тела, изгибаются в его сторону. Этот эффект, известный под названием гравитационной линзы, был предсказан Эйнштейном в 1915 г. Ньютоновская теория тоже предсказывает аналогичный эффект, но величина отклонения лучей света в ньютоновской теории гравитации в 2 раза меньше, чем в ОТО. Так происходит потому, что ньютоновская теория не учитывает кривизны трехмерного пространства, создаваемого полем гравитационной линзы, т.е. того тела, которое отклоняет лучи света. Прецизионное измерение световых геодезических линий позволяет полностью определить структуру гравитационного поля и его характеристики, включая предельную скорость гравитации. Значимый вклад в развитие теории гравитационных линз был сделан российскими физиками-теоретиками М.В. Сажиным (ГАИШ МГУ) и А.Ф. Захаровым (ИТЭФ) (Земля и Вселенная, 1993, № 2).
Предсказание Эйнштейна экспериментально проверил в 1919 г. английский астроном А. Эддингтон (1882 - 1944), который организовал специальную экспедицию для измерения эффекта отклонения лучей света в гравитационном поле Солнца. Положительный результат эксперимента Эддингтона дал начало триумфальному шествию общей теории относительности Эйнштейна по всему миру. Однако не следует забывать, что отклонение лучей света гравитационным полем Эйнштейн рассчитал для случая статического гравитационного поля, которое является очень хорошей аппроксимацией применительно к Солнечной системе. Действительно, Солнце, как уже говорилось, практически покоится в ее центре масс, и все релятивистские поправки, вызываемые его движением, пренебрежимо малы. Как сильно изменится эффект отклонения лучей света, если гравитационная линза движется? Приведет ли движение линзы к появлению принципиально новых физических эффектов?
Идея эксперимента
Общая теория относительности позволяет рассчитать гравитационное поле движущейся гравитационной линзы двумя различными методами. Первый метод заключается в решении статических уравнений Эйнштейна в неподвижной системе координат, по отношению к которой линза покоится, с последующим применением преобразования Лоренца для перехода от статического решения к движущейся системе координат. Второй метод заключается в применении нестационарных уравнений Эйнштейна для нахождения гравитационного поля линзы непосредственно в движущейся системе координат. В первом случае уравнения Эйнштейна не содержат производных по времени от гравитационных потенциалов (они равны нулю в силу статичности поля), а во втором - содержат. В каждую производную по времени в теории относительности входит фундаментальная константа, численно равная скорости света. Однако раз мы имеем дело с уравнениями гравитационного поля (которые не связаны со светом), данная константа должна быть физически интерпретирована как скорость распространения гравитационного поля (скорость гравитации). Решая уравнения Эйнштейна в равномерно движущейся системе координат, мы получаем запаздывающее гравитационное поле, где запаздывание определяется величиной скорости гравитации (но не света, так как уравнения Эйнштейна относятся только к гравитационному полю!). Интересно, что свободные гравитационные волны при этом отсутствуют, а скорость гравитации появляется в этом решении в качестве константы, определяющей величину производных по времени от гравитационного поля. Эти производные могут быть переписаны как функции запаздывающего времени, зависящего от скорости гравитации. Запаздывающее время определяет характеристики уравнений Эйнштейна, то есть те изотропные направления в пространстве, вдоль которых распространялись бы гравитационные волны, если бы они реально присутствовали. Лоренцевское преобразование характеристик уравнений Эйнштейна от неподвижной к движущейся системе координат получила название аберрации гравитации по аналогии с аберрацией света, которое есть следствие лоренцевского преобразования уравнений Максвелла.
Предположим, что мы решили уравнения Эйнштейна для гравитационной линзы в неподвижной системе координат и, применив преобразование Лоренца, перешли к движущейся. Если бы скорость гравитации в уравнениях Эйнштейна, определяющая величину запаздывания гравитационного поля, не совпадала по величине с предельной скоростью преобразований Лоренца, то поле движущейся гравитационной линзы, полученное путем преобразования Лоренца, отличалось бы от поля, полученного путем решения уравнений Эйнштейна непосредственно в движущейся системе координат. Величина рассогласования двух полей определяется разностью между скоростью гравитации и света. Для измерения этого возможного рассогласования между двумя скоростями необходимо исследовать поведение световых геодезических, используемых как реперные линии, по отношению к которым измеряется аберрация характеристик гравитационного поля. При этом максимальная величина рассогласования определяется в общей теории относительности амплитудой первых производных по времени от гравитационных потенциалов.
Суть нашего эксперимента заключалась в измерении запаздывания (аберрации) гравитационного поля, посредством наблюдения релятивистского отклонения радиоволн, идущих от квазара, Юпитером, который рассматривался как движущаяся гравитационная линза.
Влияние производных по времени на отклонение лучей света проявляется в том, что Юпитер отклоняет лучи света своим гравитационным полем не мгновенно, а с запаздыванием, обусловленным конечностью скорости распространения гравитационного поля от Юпитера до световой частицы (фотона). Такое запаздывание обусловлено волновой природой уравнений Эйнштейна и полностью совместимо с преобразованием Лоренца для них. Это преобразование - другой математический способ, подтверждающий конечность скорости распространения гравитационных полей (численно равной скорости света, согласно ОТО). Измеряя величину производных по времени в уравнениях световых геодезических, мы устанавливаем предел на величину скорости гравитации по отношению к скорости света и подтверждаем, что уравнения Эйнштейна должны сохранять свою форму (инвариантность) при применении преобразования Лоренца.
 |
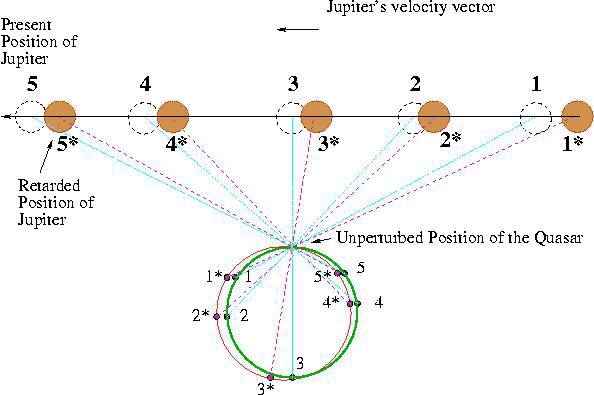
| Рис.1 - Смещение видимого положения квазара по кругу небольшого углового диаметра (кругу Эйнштейна), вследствие гравитационного отклонения лучей света, идущих от квазара, движущимся Юпитером. Предельная скорость гравитации полагается равной бесконечности. |
 |
| Рис.2 - Малое смещение и вращение круга Эйнштейна относительно невозмущенного положения квазара, вследствие аберрации гравитационного поля движущегося Юпитера. Каждая точка смещенного круга получена из точки на круге Эйнштейна путем трансляции на малое расстояние в картинной плоскости неба. Величина трансляции состоит из двух слагаемых, одна из которых направлена в сторону движения Юпитера, а другая по линии, соединяющей Юпитер и невозмущенное положение квазара. Это явление также может быть интерпретировано как "увлечение" лучей света гравитационным полем Юпитера. Предельная скорость гравитации полагается равной скорости света. |
Юпитер, проходя на небесной сфере "вблизи" квазара, отклоняет лучи света, идущие от него, смещая видимое положение данного космического радиоисточника в другую точку неба. Такое смещение в первом (статическом) приближении предсказано Эйнштейном. Оно обратно пропорционально угловому расстоянию между Юпитером и квазаром и не зависит от скорости гравитации. По мере движения Юпитера по орбите видимое положение квазара на небе смещается по кругу очень небольшого углового размера. Назовем его кругом Эйнштейна. Уравнения Эйнштейна в совокупности с уравнениями световых геодезических показывают, что Юпитер отклоняет лучи света с запаздыванием, учитывающим тот факт, что гравитационное влияние на луч света не может происходить мгновенно, а требует времени, за которое гравитационное поле проходит расстояние от источника поля до световой частицы - фотона. Это запаздывание приводит к изменению картины смещения видимого положения квазара на небе. Геометрически это соответствует малому вращению и смещению круга Эйнштейна относительно астрометрического положения квазара, невозмущенного гравитационным полем Юпитера. Величина этого смещения обратно пропорциональна квадрату углового расстояния между Юпитером и квазаром, умноженному на отношение орбитальной скорости Юпитера к скорости гравитации. Таким образом, измерение величины смещения круга Эйнштейна гравитационным полем движущегося Юпитера позволяет определить скорость гравитации, так как остальные наблюдаемые параметры хорошо известны. Особо подчеркнем, что никаких свободных гравитационных волн, излучаемых Юпитером, мы не детектировали - они существуют, но их эффект слишком мал и не мог быть измерен, о чем мы непосредственно и объявили на пресс-конференции, данной нами в Сиэтле в январе 2003 г. К сожалению, некоторые физики, как, например, Клиффорд Вилл (Университет Вашингтона, г. Сент Луис), не присутствовавшие на пресс-конференции, неправильно интерпретировали результаты эксперимента, полагая, что мы говорим об эффекте, производимом гравитационными волнами.
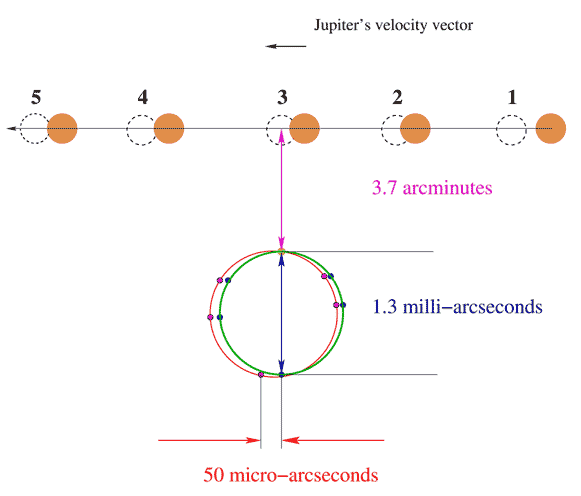 |
| Рис.3 - Величина измеряемого эффекта деформации круга Эйнштейна обусловленная конечностью величины скорости гравитации. Эта величина, предсказанная ОТО, составляла величину 50 мкс. |
Это привело к публикации нескольких (концептуально неправильных) работ, которые были направлены на то, чтобы доказать нашу "неправоту", и совершенно запутали многих физиков всего мира. В течение прошедшего года происходило постепенное прояснение данного недоразумения, которое, вне всякого сомнения, принесло большую пользу для существенного углубления и понимания теории эксперимента.
Наш эксперимент по измерению скорости гравитации был проведен 8 сентября 2002 г. Минимальное угловое расстояние между Юпитером и квазаром было 3.7', максимальное отклонение лучей света (диаметр круга Эйнштейна) составило величину 1.3 мс, а искажение круга Эйнштейна, обусловленное конечностью скорости распространения гравитационного взаимодействия, равно приблизительно 50 мкс. Цель эксперимента заключалась в измерении этой крошечной величины, примерно равной углу, под которым виден человек на Земле с расстояния в одну астрономическую единицу (расстояние от Земли до Солнца). Единственный способ измерить столь малый угол основан на применении радиоинтерферометрии со сверхдлинной базой (РСДБ).
Радиоинтерферометрия со сверхдлинной базой
Метод радиоинтерферометрии со сверхдлинной базой для измерения малых углов на небесной сфере был впервые предложен в 1965 г. советскими учеными Н.С. Кардашевым, Л.И. Матвеенко и Г.Б. Шоломицким (Земля и Вселенная, 2003, № 4). Принципиально новый тип радиоинтерферометра с независимой регистрацией данных несколькими антеннами, разнесенными на большие (межконтинентальные) расстояния, помог получить ранее немыслимое угловое разрешение, в десятки тысяч раз превышающее разрешение оптических телескопов. Блестящая новаторская идея советских радиоастрономов вскоре была реализована на нескольких зарубежных и отечественных радиотелескопах.
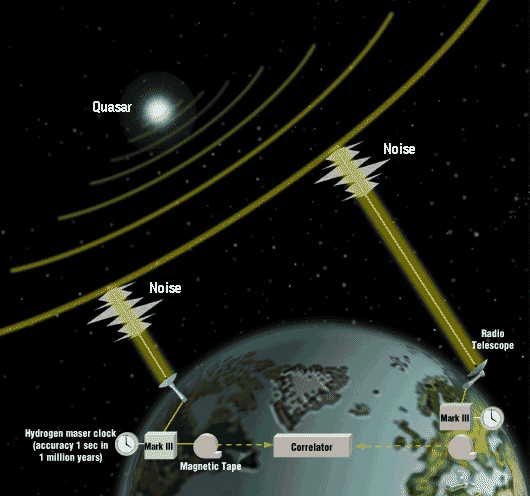 |
| Рис.4 - Радиоинтерферометрия со сверхдлинной базой. Метод основан на синхронном приеме двумя (или несколькими) антеннами, расположенными на межконтинентальном расстоянии друг от друга, радиосигнала от удаленного радиоисточника. Радиосигнал записывается на магнитные ленты, которые обрабатывают на корреляторе. Коррелятор находит временнyю задержку в приеме радиосигнала на более удаленной от радиоисточника антенне, что позволяет определить направление на него с точностью до 10 мкс дуги. |
В настоящее время наибольшее угловое разрешение достигается на американской РСДБ системе, называемой VLBA и состоящей из 10 радиотелескопов (диаметр каждого 25 м). Радиотелескопы расположены по всей территории США, включая Гаваи. Максимальная длина базы данного радиоинтерферометра около 7000 км, угловое разрешение положения радиоисточников на небе достигает величины 50 - 100 мкс дуги. Однако такое разрешение недостаточно для измерения эффекта запаздывания в положении Юпитера, обусловленного конечностью скорости гравитации. Нам необходимо было достичь точности измерения углов не менее 10 мкс дуги. Измерять такие малые углы очень трудно ввиду турбулентности земной атмосферы, приводящей к сильным случайным флуктуациям интенсивности света (мерцание) и видимого положения радиоисточников на небесной сфере, которые и ограничивают точность измерения VLBA до 50 - 100 мкс дуги. Чтобы преодолеть барьер, поставленный атмосферой, необходимо применять специальную фазово-калибровочную методику, в основном аналогичную методу адаптивной оптики (Земля и Вселенная, 2003, №1), применяемому в оптической астрономии. Суть фазово-калибровочного метода радиоинтерферометрических измерений состоит в том, что основной источник радиоизлучения наблюдается одновременно с другим радиоисточником, близко расположенным к основному. Радиоволны от двух радиоисточников проходят через одну и ту же область атмосферы и подвергаются практически одинаковому флуктуационному смещению, так что относительное угловое расстояние между источниками остается неизменным. Это позволяет устранить помехи, вызываемые мелкомасштабными колебаниями земной атмосферы, и повысить точность относительных измерений углов на небе до 20 - 30 мкс дуги.
Эксперимент и его результаты
Я познакомился с доктором Эдвардом Фомалонтом в 1996 г. во время работы по контракту в университете Хитоцубаши (Токио) и Японской Национальной Обсерватории (Митака, Токио). Эдвард приехал на один год для работы в Японском Институте Космических Исследований по программе японского космического интерферометра (VSOP). Я хорошо знал его работы по измерению релятивистского отклонения радиоволн от квазара в поле Солнца, которые он выполнил совместно с Ричардом Шрамеком в 1976-77 гг. На протяжении многих лет эти работы не были превзойдены по точности астрометрических измерений.
Моя следующая встреча с Эдвардом произошла спустя несколько лет в 2001 г. в США, куда я переехал со своей семьей для работы в университете штата Миссури (г. Колумбия). Размышляя над различными способами измерения предельной скорости распространения гравитационного взаимодействия, я пришел к выводу, что наиболее приемлемым небесным телом, которое помогло бы провести такое измерение, является Юпитер. Необходимость измерять угловое отклонение лучей света с точностью до 10 мкс дуги поставило меня перед трудной задачей выбора специалиста в области радиоинтерферометрии со сверхдлинной базой. К счастью, Эдвард продолжал (и продолжает) активно интересоваться релятивистскими экспериментами, требующими беспрецедентной точности, и с радостью согласился сотрудничать.
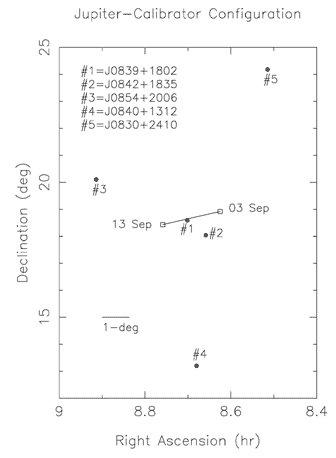
Поиск событий близких угловых сближений Юпитера с квазарами провел по моей просьбе сотрудник Государственного астрономического института им. П.К. Штернберга, доктор физико-математических наук С.М. Кудрявцев, который нашел, что наиболее оптимальное сближение произойдет 8 сентября 2002 г., когда Юпитер будет проходить вблизи квазара J0842 + 1835 на угловом расстоянии 3.7'. Времени до этого момента оставалось совсем немного - полтора года, и нам пришлось готовиться к эксперименту ударными темпами.
В начале февраля 2001 г. я поехал на международное совещание по радиоинтерферометрии, организованное NASA в американском космическом центре имени Годдарда, и представил результаты моих теоретических изысканий в докладе, который вызвал небывалый интерес и оживленную дискуссию. Все участники совещания горячо поддержали идею эксперимента и рекомендовали немедленно подать заявку для наблюдений на американской радиоинтерферометрической системе VLBA. Так я и поступил, вернувшись с совещания в свой университет. Мы с Эдвардом запросили комиссию по наблюдениям на VLBA предоставить нам время для проведения тестовых измерений и основного эксперимента. Наша заявка была полностью поддержана Национальной Радиоастрономической Обсерваторией США. Нам также оказал поддержку радиоастрономический институт им. Макса Планка в Германии. Его 100-м полноповоротная антенна, расположенная вблизи г. Бонна, в местечке Эффельсберг, принимала активное участие в эксперименте, обеспечивая минимальное время наблюдения квазара, равное всего 1 мин, что было весьма существенным фактором, для достижения необходимого углового разрешения.
Мы разработали модернизированный вариант фазово-калибровочного метода радиоинтерферометрических измерений. Стандартный метод использует только один калибровочный источник, но в нашем случае этого было недостаточно. Мы собирались измерять не просто величину смещения опорного квазара в плоскости неба, но и направление смещения, чтобы измерить величину деформации круга Эйнштейна для установления верхнего предела скорости гравитации. Таким образом мы выбрали четыре калибровочных квазара, два из которых были расположены почти на одной прямой с основным. Угловое расстояние между основным и калибровочными квазарами приблизительно равно 1°. Этот угол достаточен, чтобы гравитационное поле Юпитера практически не влияло на видимые положения калибровочных квазаров. Мы провели серию тестовых измерений за несколько месяцев до основного эксперимента и решили использовать только два калибровочных квазара (J0842 + 1835 и J0854 + 2006), что обеспечивало нам более длительное накопление сигнала от каждого из них с соответствующим увеличением точности наблюдений.
 |
--> ЧИТАТЬ ПОЛНОСТЬЮ <-- К-во Просмотров: 171
Бесплатно скачать Статья: Фундаментальный предел скорости гравитации и его измерение
|