Статья: Колебания продольные… и рождение неопределённости
И то же самое имеем для потока энергии. Можно преобразовать движение текущей энергии произвольным образом, добавляя к вектору Пойнтинга другой вектор (u, v, w), обязанный удовлетворять лишь уравнению несжимаемых жидкостей
Откуда: 
Теорема Пойнтинга , являющаяся следствием общих уравнений, ничего к ним не добавляет.
Поэтому локализация энергии логически бесполезна (а иногда, вредна).
Но имеется аспект, в котором важно рассмотреть теорему Пойнтинга.
Основным фактом, из которого проистекает закон сохранения энергии, был и остаётся экспериментально найденный факт невозможности вечного движения , факт – независимо от наших идей, и может, быть отнесён к порциям энергии, которой должен обладать эфир в отсутствие материальных тел.
Закон сохранения энергии [4], в его классической форме W = Const , объясняет эту невозможность.
Теорема Пойнтинга , требующая возможности преобразования объёмного интеграла (отчасти произвольного) в поверхностный, выражает гораздо меньше. Она легко допускает создание вечного движения, не будучи способна показать его невозможность !
По сути, пока мы не введём гипотезу запаздывающих потенциалов , непрерывное выделение энергии сходящихся волн, приходящих из бесконечности, остаётся столь же вероятным, сколь и потеря энергии, наблюдаемая в действительности.
Если бы двигатель мог вечно забирать одну лишь энергию эфира, независимо от присутствия материальных тел, то могло бы существовать и вечное движение . Таким образом, становится ясно, что прежде чем принять формулу запаздывающих потенциалов, мы должны доказать, что ускоренная частица теряет энергию и в результате подвергается противодействию, пропорциональному производной ее ускорения [13].
Достаточно лишь изменить знак c , чтобы прийти к гипотезе сходящихся волн.
Тогда мы обнаружим , что знак вектора излучения также изменится, и новая гипотеза приведёт, скажем, в случае вибрирующей частицы, к постепенному увеличению амплитуды с течением времени, а в целом – к увеличению энергии системы?!
В Природе солитоны бывают:
– на поверхности жидкости первые солитоны, обнаруженные в природе, иногда считают таковыми волны цунами
– различные виды гидроудара
– звуковые ударные – преодоление «сверхзвука»
– ионозвуковые и магнитозвуковые солитоны в плазме
– солитоны в виде коротких световых импульсов в активной среде лазера
– предположительно, примером солитона является Гигантский гексагон на Сатурне
– можно рассматривать в виде солитонов нервные импульсы [32], [49].
Математическая модель, уравнение Кортевега-де Фриза.
Одной из простейших и наиболее известных моделей, допускающих существование солитонов в решении, является уравнение Кортевега-де Фриза:
ut + uux + βuxxx = 0.
Одним из возможных решений данного уравнения является уединённый солитон :
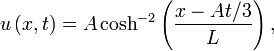но и здесь осцилятором является гармоническая функция
Кубическое уравнение Шрёдингера
Для нелинейного уравнения Шрёдингера:
