Статья: Метод АВИ в математической теории переноса вредных веществ в гетерогенных средах

. (11)

Таким образом, концентрация вредных веществ с точностью до будет.

. (12)

Так как не зависит от , отсюда вытекает, что

, (13)

где некоторая постоянная величина (в частности ).

Рассмотрим уравнение (13) при ; тогда

.

Решая уравнение Гамильтона–Якоби (13), найдем функцию :

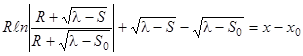, (14)

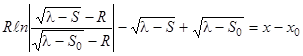, (15)

где . Из данных соотношений определяется .

Если , тогда уравнение (1) редуцируется к уравнению с постоянными коэффициентами:

. (16)

Решение однородного уравнения (16) будем искать методом разделения переменных. Пусть тогда из (16) получим

. (17)

Из (17) следует

(18)

где собственное значение.

Из (18) следует: , . Раскрывая производные, получаем:

. (19)

С точностью до из (19) получим

. (20)

Положим , тогда, подставляя это выражение в (20), получаем:

. (21)

Пусть , подставим данное выражение в правую часть уравнений (21). Приравнивая нулю коэффициенты при , в результате получаем систему рекуррентных уравнений:

(22)

из которой можно определить