Статья: О парадоксе существования волн электромагнитного поля и их способности переноса полевой энергии

Справедливости ради уместно сказать, что впервые о реальности магнитной поперечной волны с двумя ее компонентами и , сдвинутыми при распространении по фазе колебаний на , почти 30 лет назад официально в виде приоритета на открытие заявил Докторович [5], и данный факт он с удивительным упорством, достойным лучшего применения, безуспешно пытается донести до других все эти годы. Печально, но только Время – высший судия, и именно оно расставит всех по своим местам!

Полностью аналогичные рассуждения для пакета плоской волны векторного потенциала с компонентами и в системе (6) дают и , откуда снова получаем известное выражение А потому для среды идеального диэлектрика () дисперсионное соотношение для уравнений (6) есть при комплексных амплитудах в волновых решениях этой системы: 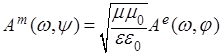, где сами решения описывают плоские однородные волны, компоненты поля которых, как и в случае ЭМ волн, синфазно распространяются в пространстве.

Как видим, именно уравнения поля ЭМ векторного потенциала (6) описывают волны, переносящие в пространстве поток момента импульса , которые со времен Пойнтинга безуспешно пытаются описать с помощью уравнений ЭМ поля (1) (см. анализ в [6]). В этой связи укажем на пионерские работы [7], где обсуждается неэнергетическое (информационное) взаимодействие векторного потенциала со средой при передаче в ней потенциальных волн и их детектирование с помощью эффекта, аналогичного эффекту Ааронова-Бома.

Согласно соотношениям (5), синфазные между собой компоненты волны поля ЭМ векторного потенциала имеют сдвиг по фазе колебаний на относительно также синфазных между собой компонент волны ЭМ поля, тем самым, приводя к вышеуказанной специфике в поведении компонент полей электрической и магнитной волн. Система соотношений (5) иллюстрирует также другой непреложный факт, что существование и распространение поля ЭМ векторного потенциала невозможно без сопутствующего ему ЭМ поля, причем, как установлено выше, перенос синфазными компонентами указанных полей потока соответствующей физической величины посредством обычного волнового процесса принципиально невозможен, он реализуется опосредованно в виде так называемых псевдоволн .

Для проводящей среды в асимптотике металлов (), как показал анализ [8], распространение волн всех четырех электродинамических составляющих реального электромагнитного поля подчиняется теоретически хорошо изученному закону для плоских волн ЭМ поля в металлах [1], где все волновые решения имеют вид экспоненциально затухающих в пространстве плоских волн со сдвигом фазы между компонентами на .

Однако вернемся к анализу энергетики распространения составляющих реального электромагнитного поля в виде плоских волн в однородной диэлектрической среде без потерь (). Вначале обратимся к закону сохранения электрической энергии , соотношение которого согласно (10) запишется как:

. (12)

Выясним, выполняется ли это выражение для плоской монохроматической электрической волны , полевые компоненты которой, согласно волновым решениям уравнений системы (7), обладая сдвигом фазы на , имеют следующий вид: и . Тогда, подставляя их в соотношение (12), приходим к соотношению:

.

Такой результат вполне удовлетворяет закону сохранения электрической энергии , поскольку усреднение по времени этого соотношения дает

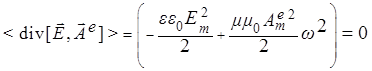. (13)

Итак, в случае электрического поля мы приходим к физически разумному результату, когда посредством электрической волны переносится чисто электрическая энергия , в рассматриваемом случае не зависящая от времени и точек пространства. Таким образом, распространение электрической волны , как и следовало ожидать, отвечает логике наших рассуждений и действительно удовлетворяет закону сохранения энергии .

Соответственно, для магнитного поля , распространяющегося в однородной среде без потерь, закон сохранения магнитной энергии согласно (11) запишется в виде соотношения:

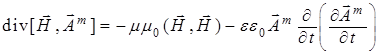. (14)

Рассмотрим, как выполняется этот закон для плоской монохроматической магнитной волны , полевые компоненты которой, согласно волновым решениям уравнений (8), имеют следующий вид: и . Подставляя их в соотношение (14) и проводя аналогичные рассуждения как при выводе формулы (13), получаем в итоге:

. (15)

Итак, в случае магнитного поля снова приходим к физически здравому результату, когда в пространстве без потерь посредством магнитной волны переносится чисто магнитная энергия , не зависящая от времени и точек пространства. Следовательно, распространение магнитной волны также удовлетворяет закону сохранения энергии .

Таким образом, аргументированно установлено, что в Природе объективно существует сравнительно сложное и необычное с точки зрения современных представлений вихревое четырехвекторное поле в виде совокупности функционально связанных между собой четырех полевых компонент , и , . Это поле, условно названное реальным электромагнитным полем , реализуется четверкой составляющих его электродинамических полей, состоящих из пар вышеуказанных компонент: электрическое поле с и , магнитное поле с и , электромагнитное поле с и , наконец, поле векторного потенциала с и . Однако способностью к непосредственному распространению в пространстве в виде волн, отвечающих обычным физическим представлениям о волновом процессе, обладают только электрическое и магнитное поля за счет наличия у этих волн сдвига фазы на между их компонентами и , соответственно, и . Реализация же собственно волн ЭМ поля и ЭМ векторного потенциала невозможна в принципе, хотя сами эти поля, как показано выше, существуют и распространяются опосредованно в виде псевдоволн , поскольку их синфазные компоненты являются составной частью компонент электрической и магнитной волн , распространяющихся обычным образом.

Тем самым все составляющие реального электромагнитного поля объективно перемещаются в пространстве совместно в виде единого волнового процесса, при котором переносятся электрическая энергия , магнитная энергия , ЭМ энергия на единицу частоты и момент ЭМ импульса . Важно понимать, что с концептуальной точки зрения разделение реального электромагнитного поля на составляющие его поля весьма условно и является переходным во времени, поскольку это в определенной мере диктуется общепринятыми физическими представлениями и современной практикой аналитического описания явлений электромагнетизма.

К сожалению, в настоящее время существующими методами регистрации электродинамических полей реально можно наблюдать только псевдоволны “обычного” ЭМ поля, компоненты и которых синфазно распространяются в пространстве. И хотя реальное наблюдение волн остальных обсуждаемых здесь полей – дело будущего, объективность их существования и неоспоримая практическая значимость достоверно подтверждается принципиальной невозможностью реализации без их посредства целого ряда физических характеристик ЭМ поля, в частности, способности переноса ЭМ энергии. Как видим, застарелый парадокс в механизме существования синфазных волн ЭМ поля и их способности переноса энергии этого поля, наконец, успешно и весьма кардинально разрешен, а результаты проведенных исследований представляют собой серьезную концептуальную модернизацию основных физических воззрений на структуру и свойства ЭМ поля в классической электродинамике.

Литература

1. Матвеев А.Н. Электродинамика. М.: Высшая школа, 1980.

2. Пирогов А.А. // Электросвязь. 1993. №5. С. 13-14.

3. Сидоренков В.В. // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2006. № 1. С. 28-37; // Материалы IX Международной конференции «Физика в системе современного образования». Санкт-Петербург: РГПУ, 2007. Секция “Профессиональное физическое образование”. С. 127-129; // Вестник Воронежского государственного технического университета. 2007. Т. 3. № 11. С. 75-82.

4. Сидоренков В.В. // http://revolution./physics/00023052.html .

5. Докторович З.И. // Заявленное открытие "Магнитные поперечные волны" приоритетная справка 32-ОТ №10247, дата поступления 5 мая 1980 г.; // http ://www.scitec library . ru / rus / catalog / pages /4797. html .

6. Соколов И.В. // УФН. 1991. Т. 161. № 10. С. 175-190.