Статья: О псевдоволнах электромагнитного поля
Общепринятая логика обсуждения вопроса о переносе энергии электромагнитного поля посредством волн такова, что проблемы здесь как бы и нет: всем все понятно, однако в действительности проблема выяснения физического механизма переноса энергии синфазными компонентами электромагнитной волны реально существует, и для разрешения парадокса требуется эвристический, кардинальный подход.
Концепция электромагнитн ого (ЭМ) поля является основополагающей в классической электродинамике [1], где считается, что все явления электромагнетизма физически полно представлены этим полем, свойства которого исчерпывающе описываются системой электродинамических уравнений Максвелла:
(a) ![]() , (b)
, (b) ![]() , (1)
, (1)
(c)  , (d)
, (d) ![]() ,
,
где ![]() - постоянная времени релаксации заряда в среде за счет ее электропроводности. Важнейшим следствием уравнений (1) является тот факт, что компоненты ЭМ поля, электрическая
- постоянная времени релаксации заряда в среде за счет ее электропроводности. Важнейшим следствием уравнений (1) является тот факт, что компоненты ЭМ поля, электрическая ![]() и магнитная
и магнитная ![]() напряженности, перемещаются в свободном пространстве в виде поперечных волн.
напряженности, перемещаются в свободном пространстве в виде поперечных волн.
С целью ответа на вопрос, как распространяются эти волны и что они переносят, обратимся к закону сохранения энергии, аналитическую формулировку которого можно получить при совместном решении уравнений Максвелла (1) в виде так называемой теоремы Пойнтинга:
![]() . (2)
. (2)
Поскольку далее рассматривается распространение ЭМ волн в среде идеального диэлектрика (![]() ), то соотношение (2) этом случае запишется как:
), то соотношение (2) этом случае запишется как:
![]() . (3)
. (3)
Рассмотрим выполнение закона сохранения энергии для монохроматической ЭМ волны, полевые компоненты которой, согласно волновым решениям уравнений Максвелла [1], распространяются, например, вдоль оси x в пространстве без потерь синфазно: ![]() и
и ![]() , а их амплитуды связаны между собой как
, а их амплитуды связаны между собой как ![]() . Подставляя выражения для этих компонент в соотношение (3), окончательно получаем:
. Подставляя выражения для этих компонент в соотношение (3), окончательно получаем:
![]() . (4)
. (4)
В итоге ![]() , так как, по определению, это объемная плотность потока векторного поля в данной точке, а потому для бегущей волны в пространстве без потерь усредненный по времени поток ее энергии через замкнутую поверхность очевидно равен нулю. Итак, уравнения Максвелла описывают необычные, весьма странные волны, которые логично назвать псевдоволнами, поскольку, с одной стороны, синфазные волны не способны в принципе переносить ЭМ энергию, а с другой - перенос энергии реально наблюдается, более того это физическое явление широко и всесторонне используется практически, определяя многие аспекты жизни современного общества .
, так как, по определению, это объемная плотность потока векторного поля в данной точке, а потому для бегущей волны в пространстве без потерь усредненный по времени поток ее энергии через замкнутую поверхность очевидно равен нулю. Итак, уравнения Максвелла описывают необычные, весьма странные волны, которые логично назвать псевдоволнами, поскольку, с одной стороны, синфазные волны не способны в принципе переносить ЭМ энергию, а с другой - перенос энергии реально наблюдается, более того это физическое явление широко и всесторонне используется практически, определяя многие аспекты жизни современного общества .
Итак, имеем парадокс, существующий уже более века. Поражает здесь то, что общепринятая логика анализа переноса энергии ЭМ волнами такова, что проблемы как бы и нет: всем все понятно. Например, из соотношения для амплитуд в волновых решениях уравнений (1) ![]() формально следует, что для ЭМ энергии
формально следует, что для ЭМ энергии ![]() , хотя синфазные волны переносить энергию не могут. Правда, делались попытки действительно разобраться в этом вопросе, но эти объяснения (например, [2]), на наш взгляд, не выдерживают критики, поскольку обсуждались не сами уравнения Максвелла или их прямые следствия, а то, что эти уравнения не учитывают характеристики реальных ЭМ излучателей или специфику взаимодействия материальной среды с ЭМ полем при распространении его волн. Это, по мнению авторов, и создает сдвиг фазы между компонентами на
, хотя синфазные волны переносить энергию не могут. Правда, делались попытки действительно разобраться в этом вопросе, но эти объяснения (например, [2]), на наш взгляд, не выдерживают критики, поскольку обсуждались не сами уравнения Максвелла или их прямые следствия, а то, что эти уравнения не учитывают характеристики реальных ЭМ излучателей или специфику взаимодействия материальной среды с ЭМ полем при распространении его волн. Это, по мнению авторов, и создает сдвиг фазы между компонентами на ![]() .
.
Для большей убедительности нашей аргументации напомним основные представления о переносе энергии посредством волнового процесса, например, рассмотрим распространение волн от брошенного в воду камня. Частицы воды массой m, поднятые на гребне волны на высоту h, имеют запас потенциальной энергии ![]() , а через четверть периода колебаний, когда гребень волны спадает, в соответствии с законом сохранения энергии потенциальная энергия частиц воды переходит в кинетическую энергию их движения
, а через четверть периода колебаний, когда гребень волны спадает, в соответствии с законом сохранения энергии потенциальная энергия частиц воды переходит в кинетическую энергию их движения ![]() , где скорость частиц
, где скорость частиц ![]() . Наличие взаимодействия молекул воды и приводит к возбуждению механической поверхностной поперечной волны. К сожалению, вышесказанное для синфазных волновых компонент ЭМ поля, описываемых уравнениями Максвелла (1), это невозможно в принципе.
. Наличие взаимодействия молекул воды и приводит к возбуждению механической поверхностной поперечной волны. К сожалению, вышесказанное для синфазных волновых компонент ЭМ поля, описываемых уравнениями Максвелла (1), это невозможно в принципе.
Однако последовательный критический анализ именно уравнений электродинамики Максвелла [3] выявил систему дифференциальных уравнений в виде соотношений первичной функциональной взаимосвязи ЭМ поля с компонентами электрической ![]() и магнитной
и магнитной ![]() напряженности и поля ЭМ векторного потенциала с электрической
напряженности и поля ЭМ векторного потенциала с электрической ![]() и магнитной
и магнитной ![]() компонентами:
компонентами:
(a) ![]() , (b)
, (b) ![]() , (5)
, (5)
(c) ![]() , (d)
, (d) 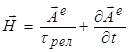 .
.
Объективность существования указанного четырехкомпонентного вихревого поля, которое физически логично назвать реальным электромагнитным полем, иллюстрируется целым рядом нетривиальных следствий из соотношений (5), поскольку математические операции над ними позволили получить три новые системы электродинамических уравнений [3], структурно аналогичных системе уравнений (1), но уже для поля ЭМ векторного потенциала с электрической ![]() и магнитной
и магнитной ![]() компонентами, электрического поля с компонентами
компонентами, электрического поля с компонентами ![]() и
и ![]() , наконец, для магнитного поля с компонентами
, наконец, для магнитного поля с компонентами ![]() и
и ![]() .
.
Подробный анализ условий распространения компонент реального ЭМ поля в виде волн представлен в работе [4], там это поле условно названо «единое электродинамическое поле». Установлено, что в среде без потерь компоненты волны вектор-потенциала совершают синфазные колебания, а у электрической и магнитной волн полевые компоненты сдвинуты между собой по фазе на ![]() . Конечно, последний результат математически тривиален, так как компоненты “обычного” ЭМ поля и поля ЭМ вектор-потенциала связаны между собой посредством производной по времени (см. соотношение (5)). Однако концептуально, с физической точки зрения данный факт весьма примечателен.
. Конечно, последний результат математически тривиален, так как компоненты “обычного” ЭМ поля и поля ЭМ вектор-потенциала связаны между собой посредством производной по времени (см. соотношение (5)). Однако концептуально, с физической точки зрения данный факт весьма примечателен.
В этой связи рассмотрим энергетические аспекты волнового распространения составляющих реального ЭМ поля, а потому приведем следующие из анализа новых систем уравнений соотношения баланса [3]:
для потока электрической энергии
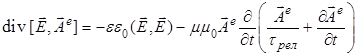 , (6)
, (6)
для потока магнитной энергии
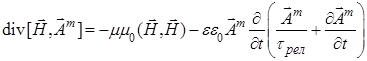 (7)
(7)
и, судя по размерности, для потока момента ЭМ импульса
![]() . (8)
. (8)
Используя представленные соотношения баланса, проведем сначала анализ энергетики перемещения в пространстве волн электрического поля на основе закона сохранения электрической энергии, соотношение баланса (6) которого запишется для среды идеального диэлектрика (![]() ) как:
) как:
![]() . (9)
. (9)
Согласно волновым решениям уравнений электрического поля [4], полевые компоненты монохроматической поперечной электрической волны имеют сдвиг фазы на ![]() :
: ![]() и
и ![]() . Тогда, подставляя их в уравнение баланса (9), приходим к следующему соотношению:
. Тогда, подставляя их в уравнение баланса (9), приходим к следующему соотношению:
--> ЧИТАТЬ ПОЛНОСТЬЮ <--