Статья: Общая постановка проблемы перекрестных эффектов
Предложена физико-математическая модель крупномасштабных перекрестных эффектов. Расчеты обобщены на теорию порядка и хаоса, устойчивости и катастроф. На основе выполненных расчетов построена дидактика явлений переноса.
Проблемы перекрестных эффектов и явлений переноса описываются в общем случае системой уравнений [1...4]:
![]() , (1)
, (1)
![]() , (2)
, (2)
![]() (3)
(3)
![]() , (4)
, (4)
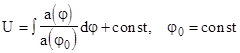 , (5)
, (5)
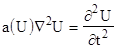 , (6)
, (6)
![]() , (7)
, (7)
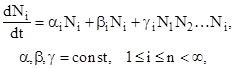 (8)
(8)
![]() , (9)
, (9)
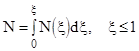 . (10)
. (10)
Формулы (1) и (2) являются следствиями второго закона И.Ньютона. Постановка Л.Онсагера (1) применима к мелкомасштабным линейным флуктуациям. Более важный практический интерес представляют формулы П.Гленсдорфа, И.Пригожина, Л.Лейбензона и др. для крупномасштабных нелинейных флуктуаций. Примером крупномасшатабных нелинейных флуктуаций являются вольт-амперная характеристика электрических цепей и индикаторные диаграммы притока идеального газа и газированной жидкости из горных пород [5].
К нелинейным крупномасштабным флуктуациям применяются формулы Гленсдорфа-Пригожина (2), которые линеаризуются с помощью так называемых квазипотенциальных функций (3) и (5).
При оценке изменения флуктуаций во времени формулы Гленсдорфа-Пригожина дополняются уравнениями математической физики (4)...(7), синергетики (8) и различными видами дельта-функции (9), (10).
Символы в формулах (1)...(10) общепринятые. В дельта-функции (9) обозначены: f - дробные значения действительного ряда чисел от нуля до единицы, t i - фиксированное время.
Поинтервальные параметры дельта-функции (9) позволили обобщить предложения автора на проблемы порядка и хаоса, катастроф и устойчивости. Формула (10) дает возможность и непрерывного определения дельта-функции.
По результатам решения уравнений (1...10) созданы методические пособия к изучению перекрестных эффектов на ЭВМ для студентов старших курсов специализации теплофизика в следующих направлениях.
Свойства квазиавтомодельности флуктуаций в локальных полях Земли.
Механика разнопеременного движения тел в поле переходных процессов.
Квазистационарность переходных процессов.
Промежуточные стадии выравнивания квазипотенциалов.
Профили термоэрозии твердых тел.
Комбинированные методы исследования переходных процессов.
Скачки потенциалов при выравнивании термодинамических сил.
Прикладные задачи перекрестных эффектов (разработка газогидратных залежей, нагревание битумов, очистка и рекультивация загрязненных участков сельскохозяйственных угодий).
Рассмотрим для примера квазиавтомодельное распределение температуры в конечных полях. Возьмем для этого автомодельное решение задачи при краевых условиях первого рода на полуплоскости:
![]() (11)
(11)
Формулу (11) можно применить и к конечным полям при соблюдении условия:
--> ЧИТАТЬ ПОЛНОСТЬЮ <--