Статья: Определение неуравновешенной радиальной силы резания при сверлении

Одним из факторов, определяющих при сверлении точность обработки отверстий, особенно глубоких, является неуравновешенная радиальная сила резания . Считается, что при идеальной заточке сверла радиальные силы резания Рy, действующие на каждый из зубьев инструмента, равны между собой и уравновешивают друг друга.

В реальной практике вследствие асимметричной заточки сверла возникает неуравновешенная радиальная сила резания , вызывающая изгиб инструмента и приводящая к возникновению дополнительных погрешностей в продольном сечении обрабатываемых отверстий. В настоящее время не существует общепринятой методики для определения силы . В работе предпринята попытка показать, что эта сила зависит не только от твердости обрабатываемого материала (что широко известно), но также от конструктивных параметров режущего инструмента и принятых режимов обработки.

Анализ сил, возникающих при обработке резанием, показывает, что радиальная сила резания Рy может быть определена из рис. 1 зависимостью [1]:

, (1)

где РN – составляющая силы резания, направленная по нормали к режущей кромке инструмента; – главный угол в плане, – угол отклонения стружки. Принимают: знак «плюс» при отрицательном значении угла , и знак «минус» при положительном значении угла .

Зависимость (1) для определения радиальной силы не учитывает изменения геометрических параметров инструмента вдоль режущей кромки, что является характерным для сверла.

Сила РN представляет собой одну из составляющих силы Рz и может быть рассчитана [1, 2] по выражению

, (2)

где Рz – сила, действующая в направлении главного движения; – угол скалывания. При обработке пластичных материалов можно принимать при расчетах

, (3)

где – переднии угол в нормальной секущей плоскости.

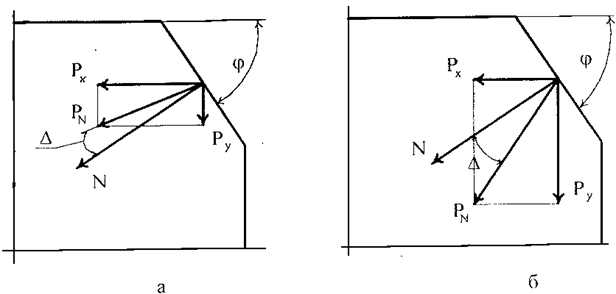
Рисунок 1 – К определению силы Рy: а – отрицательное значение угла ; б – отрицательное значение угла .

Сила Рz может быть определена из выражения

, (4)

где – предел прочности на растяжение обрабатываемого материала; Sz – подача на зуб сверла; t – глубина резания.

Глубина резания при сверлении [3] принимается равной радиусу обрабатываемой поверхности: t=0,5D, где D – диаметр сверления.

Рассмотрим определение угла отклонения стружки , являющегося одним из параметров при определении радиальной составляющей силы резания Py. При несвободном резании и угле наклона главной режущей кромки угол отклонения стружки следует вычислять по формуле

, (5)

где – вспомогательный расчетный угол, значение которого определяется зависимостью

, (6)

где – вспомогательный угол в плане; при сверлении: .

Известно, что некоторые параметры, характеризующие процесс резания, являются переменными в зависимости от положения произвольной точки А режущей кромки сверла, в которой они измеряются. Величина угла определяется зависимостью

, (7)

где rc и rx – соответственно радиус сердцевины сверла и текущий радиус произвольной точки режущей кромки. – угол наклона стружечной канавки.

Необходимые для последующего анализа расчетные зависимости геометрических параметров , и определяют на основании данных работ [4, 5].

Угол наклона главной режущей кромки:

, (8)

где ' – угол при вершине сверла.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--