Статья: Парадоксы специальной и общей теорий относительности

В.И. Моренко

Abstract. This article is devoted to special relativity theory, Lorentz transformations and curvature of space-time. Isotropy and flatness of space have been experimentally proved but the theory (special and general relativity theories) demands different determination of space-time properties. Reasons of such disagreement are hidden in mathematical tools and methods used by the theories

Специальная теория относительности основана на двух, считающихся экспериментально доказанными, фактах – конечности скорости света и ее постоянстве в различных инерциальных системах отсчета (независимости скорости света от его источника). Именно эти условия, по общему мнению, не позволяют использовать в механике преобразования Галилея при переходе от одной инерциальной системы отсчета к другой. И, как следствие, за основу математических принципов описания процессов движения принимается релятивистский принцип относительности, основанный на преобразованиях Лоренца. Очевидность этих преобразований кажется настолько безупречной, что не должно, казалось бы, и возникать сомнений в правомерности выводов, вытекающих из применения принципа лоренц-инвариантности в физической теории.

Действительно, в соответствии с обоими постулатами специальной теории относительности (релятивистский принцип относительности Эйнштейна и принцип инвариантности скорости света в вакууме) для двух инерциальных систем отсчета K и K ’ , можно записать:

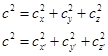
В этих уравнениях компоненты скорости света при условии прямолинейности его распространения:

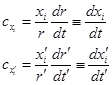
Преобразования Лоренца сохраняют инвариантность координатного времени при переходе от одной локально-инерциальной системы отсчета к другой. Однако получены эти преобразования весьма спорным образом.

Действительно, преобразования Лоренца – есть линейные преобразования координат и времени двух прямоугольных линейных координатных систем, одна из которых является неподвижной, а вторая движется относительно первой со скоростью V . Для определения соответствия координат и времен используется модель описания движения единичного пробного фотона (сигнала) из единого в нулевой момент времени для обеих систем начала координат O и в общую для обеих систем точку M . И все было бы замечательно, если бы не то обстоятельство, что траектория движения пробного фотона l _f при заданных условиях не может быть одновременно прямолинейной в обеих системах координат K и K ’ , кроме очевидного случая, когда OO ’ M – прямая линия. Данное утверждение вытекает из сравнения направления вектора прямолинейного движения пробного фотона в системе K с направлением вектора движения того же самого фотона в системе K ’ . Очевидно, что компоненты скорости фотона в системе K подчиняются уравнению:

Но в системе K ’ эти компоненты определяются выражением:

В связи с этим, уравнению в системе K :

в системе K ’ может быть противопоставлено только уравнение:

В этих обстоятельствах использование метода линейных преобразований для сравнения координат и времени систем K и K ’ является, конечно, оригинальным, но вряд ли продуктивным приемом.

Таким образом, специальная теория относительности не может быть основана на лоренц-инвариатности, но предполагает свободу выбора лабораторной системы координат, что тождественно утверждению об инвариантности математической формы определения координатного времени в различных локально-инерциальных системах координат. Сама же существующая трактовка СТО является следствием пренебрежения правилами математики (физики шутят).

В противоположность СТО в общей теории относительности математические предпочтения возобладали над физическим смыслом, хотя последствия таких предпочтений не имеют столь явного вида (математики шутят аккуратнее физиков).

В настоящее время наиболее признанным определением сущности общей теории относительности является выражение интервала:

Данное выражение трактуется как изменение свойств (мер длины) пространства в присутствии масс при сохранении величины скорости света.

Но если внимательно рассмотреть уравнение для интервала, понимая, что он не является лоренц-инвариантным, но справедлив для любой лабораторной системы координат, можно найти два способа его объяснения – математический и физический. Первый основан на геометрическом способе решения физических задач и полностью реализован в аппарате общей теории относительности и полевых теориях. А вот второй способ, основанный на возможности изменения скорости света в присутствии масс, по непонятным причинам полностью исключен из рассмотрения в физических теориях. Однако именно второй способ имеет четкое физическое обоснование, поскольку в оптике широко известно явление преломления света, вызванное уменьшением скорости распространения электромагнитных волн в физической среде; а присутствие в данном выражении члена может трактоваться и как наличие в природе масштабного фактора и как наличие у вакуума показателя преломления, величина которого в присутствии гравитационных масс отлична от величины этого параметра в отсутствии указанных масс.

Для того, чтобы сделать правильный выбор, какая из трактовок является удовлетворительной, нам необходимо разобраться, что является причиной искривления пространства – физическое явление или результат математического описания гравитационного взаимодействия.

Для этого необходимо, прежде всего, понять, о каком именно пространстве идет речь – о математическом (мысленная сущность), или о физическом (реальная сущность) гравитационном поле. То, что в уравнении поля Эйнштейна объединены физические и геометрические величины, еще не свидетельствует о физической природе искривления пространства, так как физические величины этого уравнения относятся не собственно к пространству, а к включенным в него источникам гравитационного поля. И корректным, с позиции сохранения непрерывности системы координат, на которой базируется формулировка членов из левой части уравнения поля Эйнштейна, является условие отсутствия размера у источников поля – точечная модель элементарных частиц. Отметим, что данное условие является обязательным для любого физического поля при его математическом описании известными на настоящий момент методами геометрического построения координатного пространства. Если же источник поля имеет размеры, то начало связанной с ним системы координат оказывается внутри отличной от собственно поля физической сущности – иного пространства. В этом случае возникает проблема исключения из рассмотрения внутреннего пространства и его замены на внешнее. В общей теории относительности данная проблема проявляется при возникновении в решениях уравнения поля параметра , количественно совпадающего с радиусом дырки в поле, заполненной веществом источника этого поля.

Для того, чтобы хоть как-то обеспечить соответствие математической модели (гравитационного поля) физической реальности при условии сохранения непрерывности координатной системы, можно через понятие аффинной связности ввести представление об «искривлении» пространства в присутствии гравитационных масс как способ отображения пространства с «дырками» на непрерывное пространство. Но в этом случае искривленное пространство уже не является физической сущностью, а представляет из себя некоторую адекватную математическую модель.

Таким образом, эффект искривления пространства возникает уже на этапе математического описания гравитационного взаимодействия и, в принципе, не требует дополнительно физического обоснования.

В то же время, не меняя очень удобных для математики и бытового мышления представлений о пространстве как линейной, однородной и непрерывной сущности, можно использовать наличие у элементарных частиц конечных размеров для определения показателя изменения скорости света в окрестности гравитационной массы следующим образом:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--