Статья: Планеты и законы их обращения
![]() . (1.12)
. (1.12)
Полученное выражение позволяет, по известным из наблюдений периодам обращения планет, других небесных тел вокруг Солнца, вычислять их средние гелиоцентрические расстояния.
Найденные эмпирически из наблюдательной астрономии законы Кеплера показали, что Солнечная система представляет собой механическую систему с центром, находящимся в солнечной массе.
Законы Кеплера послужили Ньютону основой для вывода своего знаменитого закона всемирного тяготения, который он сформулировал так: каждые две материальные частицы взаимно притягиваются с силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними.
Математическая формулировка этого закона имеет вид:
![]() , (I.13)
, (I.13)
где M и m – взаимодействующие массы, r – расстояние между ними; G – гравитационная постоянная. В системе СИ G = 6,672·10-11 м3·кг-1·с-2. Физический смысл гравитационной постоянной заключается в следующем: она характеризует силу притяжения двух масс весом в 1 кг каждая на расстоянии в 1 м. Величина G впервые была определена в 1798 г. английским физиком Кавендишем с помощью крутильных весов.
Закон Ньютона решил задачу о характере действия силы, управляющей движением планет. Это сила тяготения, создаваемая центральной массой Солнца. Именно эта сила не дает планетам разлететься, а сохраняет их в связной системе последовательных орбит, по которым как на привязи сотни миллионов лет кружатся большие и малые планеты.
Решая задачу движения двух тел под действием взаимного притяжения Ньютон аналитически определил законы движения планет в поле тяготения Солнца. Тем самым эмпирические законы Кеплера получили строгое математическое доказательство. Третий же закон был уточнен за счет введения масс планет и Солнца:
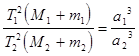 . (I.14)
. (I.14)
Теперь с его помощью оказалось возможным вычислять массы небесных тел. Полагая в выражении (I.14) массы спутников планет m1 и m2 равными нулю, ввиду их малости в сравнении с массой планет (за исключением Луны) и приняв массу Земли M2 = 1, соотношение (I.14) примет вид:
![]() . (I.15)
. (I.15)
Воспользуемся законом тяготения и определим массу Земли, полагая, что взаимодействуют две массы – Земли (М) и некоторого тела, лежащего на ее поверхности. Сила притяжения этого тела определяется законом Ньютона:
![]() . (I.16)
. (I.16)
Но одновременно из второго закона механики эта же сила равна произведению массы на ускорение:
![]() , (I.17)
, (I.17)
где g – ускорение силы тяжести; R – радиус Земли.
Приравнивая правые части выражений (I.16) и (I.17):
![]() ,
,
найдем выражение для определения массы Земли:
![]() . (I.18)
. (I.18)
Подставив в (I.18) известные значения G = 6,672·10-11 м3·кг-1·с-2,
g = 9,81 м/с2, R = 6,371·106 м, в итоге получим MЗ = 5,97·1024 кг, или в граммах: M3 = 5,97·1027 г. Такова масса Земли. Обращаем внимание на формулы (I.16), (I.17), (I.18) – их надо твердо помнить. В дальнейшем мы часто будем пользоваться ими как исходными для определения входящих в них параметров.
Теперь воспользуемся уточненным третьим законом Кеплера и найдем из выражения (I.15) массу Солнца. Для этого рассмотрим две системы тел – Солнце с Землей и Землю с Луной. В первой системе
a1 = 149,6·106 км, Т1 = 365,26 суток; во второй системе а2 = 384,4 ·103 км, Т2 = 27,32 суток. Подставляя эти значения в формулу (I.15), находим массу Солнца в относительных единицах массы Земли М0=328700 М3. Полученный результат отличается от более точных расчетов, так как в сравнении с массой Земли массу Луны нельзя приравнивать нулю (масса Луны составляет 1/81 массы Земли). Зная массу Земли в абсолютных единицах (килограммах или граммах) и взяв более точное определение массы Солнца (М0 = 333000 М3), определим его абсолютную массу: М0 = 333000·5,97·1027 г = 1,98·1033 г.
В настоящее время для более точного определения массы и фигуры планет и их спутников используются параметры орбиты искусственных спутников, запускаемых с Земли.