Статья: Потоки космических лучей в максимуме кривой поглощения в атмосфере и на границе атмосферы (1957–2007)
Рис. 2б. То же, что на рис. 2а, для разности dN2(х) скоростей счета телескопа на широтах с Rс = 0.6 ГВ и Rс = 2.4 ГВ в северном полушарии.
В качестве примера на рис. 2а, б показаны высотные зависимости разности потоков частиц dN1m(x) и dN2m(x) в минимуме солнечной активности и указан интервал энергий первичных протонов, к которому эти разности относятся. Приведены также выражения для аппроксимации величин dN1m(x) и dN2m(x), рассчитанные по методу наименьших квадратов, и значения коэффициентов корреляции r между экспериментальными точками и аппроксимацией. Разности кривых поглощения в интервале энергий 0.1 ? E ? 1.5 ГэВ удается аппроксимировать экспоненциальным законом (сплошная линия).
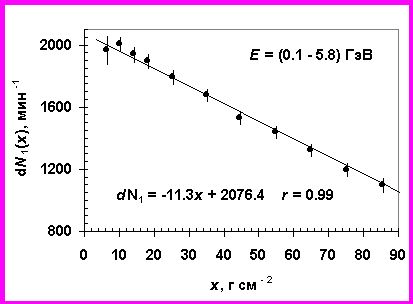

Рис. 3а. Разность скоростей счета dN1(х) одиночного счетчика на высокой широте (Rс = 0.6 ГВ) и на низкой широте (Rс = 6.7 ГВ) в северном полушарии в зависимости от х. Показаны утроенные стандартные отклонения 3σ.
Рис. 3б. То же, что на рис. 3а, для разности dN2(х) скоростей счета телескопа на широтах с Rс = 0.6 ГВ и Rс = 6.7 ГВ в северном полушарии.
Аналогичные разности высотных кривых, полученных на широтах с Rс = 0.6 ГВ и Rс = 6.7 ГВ, приведены на рис 3а, б.
В этом случае интервал энергии первичных протонов составляет 0.1 < E < 5.8 ГэВ. Величины dN1m(x) и dN2m(x) можно аппроксимировать линейным законом.
Полученные экстраполяцией потоки заряженных частиц при х = 0 включают первичные космические лучи J0 и частицы альбедо JА. Вычитая из потоков заряженных частиц потоки частиц альбедо JА, можно получить потоки первичных космических лучей J0 на границе атмосферы. Величины потоков альбедных частиц JA представлены в [8, 9]. При вычислениях предполагалось, что первичные космические лучи распределены в верхней полусфере изотропно, а геометрические факторы одиночного счетчика и телескопа равны, соответственно, 16.4 см2 и 17.8 см2.ср. Среднемесячные значения потоков первичных частиц на границе атмосферы J0(Е > 0.1 ГэВ) и J0(0.1 < Е < 1.5 ГэВ) даны в таблицах 31–32.
б) связь между потоками частиц на границе атмосферы и потоками в максимуме кривой поглощения
Отметим тот факт, что коэффициент корреляции r между относящимися к минимуму солнечной активности величинами dN1(х), dN2(х) и их аппроксимацией близок к 1 (рис. 2а, б и 3а, б). Это свидетельствует о том, что такая аппроксимация данных оправдана. Однако высокие значения r получаются не для всех периодов наблюдений. В периоды, близкие к максимумам солнечной активности, широтный эффект в атмосфере существенно уменьшается, соответственно уменьшаются разности потоков частиц dN1(х) и dN2(х), и их ошибки становятся сравнимыми с ошибками наблюдений. Особенно это заметно на разностях, полученных по измерениям на высоких и средних широтах. В эти периоды метод экстраполяции становится неточным. Кроме того, потоки космических лучей N1(х), полученные на высоких широтах с помощью одиночного счетчика, могут содержать небольшой вклад от высыпающихся частиц солнечного или магнитосферного происхождения.
Поэтому для нахождения потоков первичных частиц J0(Е > 0.1 ГэВ) и J0(0.1 < Е < 1.5 ГэВ) на границе атмосферы мы используем еще один метод, основанный на связи величин J0 с потоками частиц Nm в максимумах кривых поглощения. Как уже говорилось, величины Nm имеют минимальную статистическую погрешность и не зависят от неточности в определении атмосферного давления х. Мы используем значения Nm, полученные на станциях с геомагнитными порогами Rс, равными 0.6, 2.4 и 6.7 ГВ. Атмосферное давление хm, при котором регистрируется максимальный поток частиц, зависит от геомагнитного порога станции и от фазы 11-летнего солнечного цикла. В таблице 2 приведены значения хm и Еmin в минимуме и максимуме солнечной активности для указанных выше геомагнитных порогов. Под Еmin понимается пороговое значение энергии первичных протонов, начиная с которого они дают вклад в потоки частиц на глубине хm в атмосфере. Значения Emin для атмосферного давления xm получены из соотношения , где R = Ra = 4.10–2 при Ra > Rc и R = Rc при Ra < Rc, mp – масса протона, xm – атмосферное давление в г.см–2 xm 0.8 [7].
Таблица 2. Значения хm и Еmin (для протонов, по данным одиночного счетчика) для пунктов наблюдений с геомагнитными порогами Rc, равными 0.6, 2.4 и 6.7 ГВ, в периоды минимума и максимума солнечной активности
| Rc, ГВ (Ec, ГэВ) | 0.6 (0.18) | 2.4 (1.6) | 6.7 (5.8) | |
| Минимум солнечной активности | хm, г.×см–2 | 30 | 50 | 80 |
| Еmin, ГэВ | 0.18 | 1.6* | 5.8* | |
| Максимум солнечной активности | хm, г×см–2 | 60 | 60 | 85 |
| Еmin, ГэВ | 0.5 | 1.6* | 5.8* | |
* – значения Еmin определяются величиной порога геомагнитного обрезания Rc.
Из таблицы 2 видно, что для величин Nm значения Еmin определяются атмосферным обрезанием только в области полярных широт в максимуме солнечной активности. На средних и низких широтах минимальные значения энергий первичных частиц на границе атмосферы Еmin определяются величиной геомагнитного порога Rc.


Рис. 4а. Корреляционная связь между среднемесячными значениями первичных потоков космических лучей J0(0.1 > Е > 1.5 ГэВ), полученными методом экстраполяции за период 07.1957–06.2004, и разностями потоков частиц dN1m по данным одиночного счетчика в максимуме высотных кривых в атмосфере на широтах с Rс = 0.6 и 2.4 ГВ. Прямая линия проведена методом наименьших квадратов.
Рис. 4б. То же, что на рис. 4а, для разностей dN2m потоков космических лучей в максимумах высотных кривых в атмосфере, полученных с помощью телескопа, на широтах с Rс = 0.6 и 2.4 ГВ за период 01.1960–12.2004.
На рис. 4а, б показана зависимость между значениями первичных потоков космических лучей J0(0.1 > Е > 1.5 ГэВ), полученных методом экстраполяции, и разностями потоков частиц dN1m = N1m(0.6) – N1m(2.4) по данным одиночного счетчика и dN2m = N2m(0.6) – N2m(2.4) по данным телескопа в максимуме их высотных кривых. Соотношение между J0 и dN1m для одиночного счетчика имеет высокий коэффициент корреляции r = 0.95 и может быть представлено в виде:
J0(0.1 < E < 1.5 ГэВ) = (2773 ± 25)?dN1m + (154± 9), (1)
где [J0] = м–2.с–1.ср–1 и [dN1m] = см–2.с–1.
Для счетчикового телескопа (рис.4б) коэффициент корреляции r равен 0.93, а связь между J0 и dN2m имеет вид:
J0(0.1 < E < 1.5 ГэВ) = (19715 ± 239)?dN2m + (216± 11), (2) где [J0] = м–2.с–1.ср–1 и [dN2m]= см–2.с–1.ср–1.
Вклад частиц альбедо в величину J0, найденную по данным телескопа, незначителен. В максимуме кривых поглощения в атмосфере так же, как и на ее границе частицы распределены изотропно в верхней полусфере [3] и геометрический фактор телескопа равен Гтел = 17.8 cм2.ср.


Рис. 5а. Корреляционная связь между значениями первичных потоков космических лучей J0(Е > 0.1 ГэВ), полученными методом экстраполяции за период 07.1957–12.2004, и потоками частиц N1m, регистрируемыми одиночными счетчиками в максимумах высотных кривых в атмосфере на широте с Rc = 0.6 ГВ. Прямая линия проведена методом наименьших квадратов.
Рис. 5б. То же, что на рис. 5а, для данных, полученных с помощью телескопа на широте с Rc = 0.6 ГВ за период 01.1960–12.2004.
Аналогичные корреляционные связи между экстраполированными значениями интегральных потоков по энергии J0(Е > 0.1 ГэВ) и величинами потоков космических лучей N1m и N2m в максимумах высотных кривых можно найти для полярных широт (Rc = 0.6 ГВ). Эти связи показаны на рис. 5а, б. Для данных, полученных с помощью одиночного счетчика, коэффициент корреляции r равен 0.99, и связь между J0 и N1m имеет вид:
J0(E > 0.1 ГэВ) = (1893 ± 12)?N1m – (2778 ± 32), (3) где [J0] =м–2.с–1.ср–1 и [N1m]= cм–2.ср–1. Для данных, полученных с помощью телескопа, коэффициент корреляции r = 0.98, и связь между J0 и N2m имеет вид:
J0(E > 0.1 ГэВ) = (13051 ± 98)?N2m – (2698 ± 39), (4)