Статья: Сетевые взаимосвязи в профессиональном сообществе социологов: методика контент-аналитического исследования биографий

Аналогичные сети создаются для каждого актора. Эгоцентрические сети представляют собой экстракт биографического текста, и их информативность в определенном отношении выше информативности повествований. Вместе с тем, эгоцентрические сети остаются препарированными первичными данными, требующими обработки и анализа. Хотя в них уже можно производить элементарные подсчеты, аналогичные подсчету некоторых индивидуальных социометрических индексов, они не являются математическими моделями, и никаких обобщений отсюда не следует. Данные создаются здесь методом формирования текстового массива — это обстоятельство дает основания для сомнений в их надежности и релевантности для изучения научной коммуникации. Метод опроса дает не больше, чем может дать метод опроса. Так или иначе, следующий шаг заключается в переходе от рассказа–"случая" к генерализациям — совмещению эгоцентричных сетей и построению общей сети.

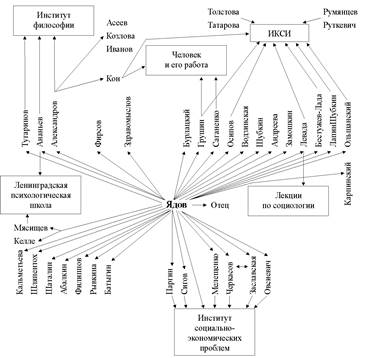
Рис. 4. Эгоцентрическая сеть профессора В.А. Ядова

Преобразование эгоцентрических сетей в общую сеть

Общая сеть строится при помощи обычной социоматрицы, вес связей определяется количеством упоминаний. При расчете структурных коэффициентов акторов (эквивалентности и центральности) весами можно пренебречь, и элементы матрицы будут обозначаться как 0 или 1. Таким образом, фиксируется наличие или отсутствие упоминания одного актора другим. В результате этих операций создается социоматрица, где выделены максимально сильные связи (табл. 1). Выделение максимальных связей очищает сеть от "шума", более четко отображает общую структуру взаимодействий. Построенная на основе социоматрицы сеть представляет собой определенную генерализацию (рис. 6).

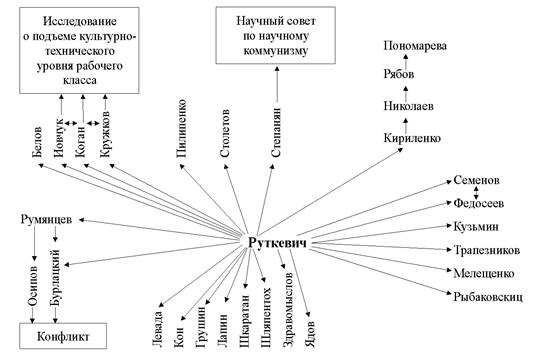
Рис. 5. Эгоцентрическая сеть члена-корреспондента РАН М.Н. Руткевича

В обобщенной сети можно выделить несколько "звезд". Это В.А. Ядов, Б.А. Грушин, Ю.А. Левада, Г.В. Осипов, М.Н. Руткевич. Опять же следует отметить, что речь идет не об их влиянии в профессиональном сообществе и, тем более, не о научных вкладах, а о репрезентации в биографических повествованиях, коллекция которых, разумеется, отражает коллективные представления части профессионального сообщества1. На основе обобщенной сети можно определить и контекст упоминания акторов, иными словами, можно подсчитать, что о ком говорят. В "положительные звезды" попадают В.А. Ядов, Б.А. Грушин, Ю.А. Левада. В "отрицательные" — М.Н. Руткевич, к Г.В. Осипову отношение менее однозначное. Можно детализировать задачу, показав, кто и в каком контексте говорит о "звездах", а также у кого какие "звезды". Контекст упоминаний о М.Н. Руткевиче получается достаточно отрицательным и связывается с так называемым погромом в Институте конкретных социальных исследований, который М.Н. Руткевич возглавил в начале 1970-х годов. Возможны и противоположные объяснения. Например, В.С. Семенов упоминает о М.Н. Руткевиче в положительном контексте. В.А. Ядова чаще всех упоминают В.В. Колбановский (10 раз), А.Г. Здравомыслов (6 раз), Б.А. Грушин (5 раз), Н.Ф. Наумова (5 раз), Г.В. Осипов (4 раза).

Таблица 1

Матрица смежных вершин (выделены сильные связи:  4)

Колбановский	Ядов	Шубкин	Левада	Осипов	Кон	Заславская	Здравомыслов	Ольшанский	Карпинский	Грушин	Оников
1	2	3	4	5	6	7	8	9	10	11	12
Колбановский	1		10	3	7	17	3	2	4	1	1	5
Ядов	2		4	6	7	10	3	3	1	1	8
Шубкин	3	1		1
Левада	4	
Осипов	5	4	2	2		1	1
Кон	6	2	
Заславская	7	1	7	1	
Здравомыслов	8	6	1	3	1	2	
Ольшанский	9	1	1	1	1	6	2	
Карпинский	10	3	1	3	8	2		4
Грушин	11	5	3	11	5		2
Оников	12	2	2	2	6	
Руткевич	13	3	3	1	2	3	10
Лапин	14	3	8	11	2	1	1	1	5	1
Рывкина	15	2	5
Коган	16	1
Наумова	17	5	4	12	1	2
Галкин	18	1	2	1	4	3	2	3	2
Пилипенко	19	1	3	3	6	3	2	2	1	3
Фирсов	20	3	1	2
Араб-Оглы	21	1	2	1	4
Гордон	22	1	1
Давыдов	23	1	1
Бестужев	24	1	4	1
Семенов	25	3	3	2
ВСЕГО		3	56	26	68	85	27	15	18	4	8	50	4

Продолжение таблицы 1

Руткевич	Лапин	Рывкина	Коган	Наумова	Галкин	Пилипенко	Фирсов	Араб-Оглы	Гордон	Давыдов	Бестужев-Лада	Семенов	ВСЕГО
13	14	15	16	17	18	19	20	21	22	23	24	25
5	12	2	2	2	2	2	1	2	2	2	87
6	2	1	1	53
1	3
2	1	3
2	1	13
2
4	6	19
2	1	16
1	13
7	2	1	1	1	33
8	2	6	1	1	44
12
	4	1	1	1	7	34
6		3	1	1	44
1		8
7		8
1	2		1	29
2	1		1	22
2	1	1	1	2		1	1	1	34
	6
	4	1	13
5		7
2		5
1	1		8
6		14
68	28	10	6	8	6	2	9	7	5	3	14	530

Таблица 2

Матрица смежных вершин (выделены взаимные связи)

Колбановский	Ядов	Шубкин	Левада	Осипов	Кон	Заславская	Здравомыслов	Ольшанский	Карпинский	Грушин	Оников
1	2	3	4	5	6	7	8	9	10	11	12
Колбановский	1		10	3	7	17	3	2	4	1	1	5
Ядов	2		4	6	7	10	3	3	1	1	8
Шубкин	3	1		1
Левада	4	
Осипов	5	4	2	2		1	1
Кон	6	2	
Заславская	7	1	7	1	
Здравомыслов	8	6	1	3	1	2	
Ольшанский	9	1	1	1	1	6	2	
Карпинский	10	3	1	3	8	2		4
Грушин	11	5	3	11	5		2
Оников	12	2	2	2	6	
Руткевич	13	3	3	1	2	3	10
Лапин	14	3	8	11	2	1	1	1	5	1
Рывкина	15	2	5
Коган	16	1
Наумова	17	5	4	12	1	2
Галкин	18	1	2	1	4	3	2	3	2
Пилипенко	19	1	3	3	6	3	2	2	1	3
Фирсов	20	3	1	2
Араб-Оглы	21	1	2	1	4
Гордон	22	1	1
Давыдов	23	1	1
Бестужев	24	1	4	1
Семенов	25	3	3	2
ВСЕГО		3	56	26	68	85	27	15	18	4	8	50	4

Продолжение таблицы 2

Руткевич	Лапин	Рывкина	Коган	Наумова	Галкин	Пилипенко	Фирсов	Араб-Оглы	Гордон	Давыдов	Бестужев-Лада	Семенов	ВСЕГО
13	14	15	16	17	18	19	20	21	22	23	24	25
5	12	2	2	2	2	2	1	2	2	2	87
6	2	1	1	53
1	3
2	1	3
2	1	13
2
4	6	19
2	1	16
1	13
7	2	1	1	1	33
8	2	6	1	1	44
12
	4	1	1	1	7	34
6		3	1	1	44
1		8
7		8
1	2		1	29
2	1		1	22
2	1	1	1	2		1	1	1	34
	6
	4	1	13
5		7
2		5
1	1		8
6		14
68	28	10	6	8	6	2	9	7	5	3	14	530

Рис. 6. Схема сильных связей в научном сообществе: максимальное остовное дерево, 23 вершины, 39 связей

В этой же матрице можно решить другую задачу: выделить не самые сильные, а взаимные упоминания (табл. 2). Сеть взаимодействий в этом случае значительно меняется. Во-первых, ее структура принимает двухполюсный вид. Сопоставив веса с контекстами, можно видеть некий аналог черно-белого изображения: "положительный" полюс представлен В.А. Ядовым, "отрицательный" — М.Н. Руткевичем. Такая сеть может показаться более информативной. Другие фигуры распознаются на черно-белом фоне не столь отчетливо. Так, несмотря на то, что Ю.А. Леваду упоминали многие информанты, он упомянул лишь немногих из них, поэтому его "звездность" отображается в сети взаимных упоминаний слабее, чем в сети сильных упоминаний. Г.В. Осипов, В.С. Семенов, Н.Ф. Пилипенко занимают промежуточное место между двумя полюсами. Сеть, построенная по принципу выделения взаимных связей (рис. 7), дает больше возможностей для применения числовых методов анализа. В частности, в данном случае можно не учитывать направление связей (сеть "взаимная") и перемещаться по сети в любом направлении. В ней нет тупиковых "висячих" вершин, в которые можно попасть при прохождении графа. Тем самым становится реализуемой задача применения таких свойств сети, как центральность и эквивалентность позиций акторов. Структурные индикаторы центральности и эквивалентности разработаны для неориентированных графов, и, применяя их, можно отказаться от весовых коэффициентов. Наличие/отсутствие связи кодируется соответственно как 1 или 0.

Центральность — местоположение актора относительно других акторов. Имеются многообразные определения центральности [9]. В одном случае центральной считается вершина, связанная с наибольшим количеством других акторов (степень центральности). В другом случае под центральной имеется в виду вершина, которая находится наиболее близко ко всем остальным вершинам (плотность центральности). В третьем случае, чем большее количество потоков перемещаемых ресурсов контролирует вершина, тем более центральной она является (посредничество центральности). Решаемая нами задача основана на третьем определении центральности.

Рис. 7. Схема взаимных связей в научном сообществе (22 вершины, 35 связей)

Мы можем рассчитать центральность актора по формуле Шимбелла-Питтса. Здесь центральность рассматривается как посредничество:

CB (ni)= , i j,k (1)

— ненормированный показатель центральности актора ni, где:

gjk – общее число кратчайших путей между вершинами nj и nk ;

gjk(ni) – число кратчайших путей между вершинами nj и nk, которые проходят через вершину ni;

i отлично от j и k.

Идеология процедуры состоит в следующем: в связном графе из любой вершины можно попасть в любую другую вершину одним или несколькими путями. Если путей несколько, то путь, который включает наименьшее количество ребер, называют кратчайшим.

Кратчайших путей тоже может быть несколько. Так, от Осипова к Лапину (имена являются обозначениями вершин) мы можем пройти следующими кратчайшими маршрутами: Осипов — Ядов — Лапин; Осипов — Здравомыслов — Лапин; Осипов — Наумова — Лапин; Осипов — Руткевич — Лапин.

Тогда одно слагаемое в формуле (1) для Ядова будет равно 1/4, так как им "контролируется" одна четвертая всех кратчайших маршрутов.