Статья: Специальная теория относительности А Эйнштейна - величайшая афера в истории физики

Тогда выражение (21) можно переписать в виде:

Сравнивая (22) с (10) видим, что “сокращение Фиджеральда” прямо взаимосвязано с сокращением длины волны Де Бройля. Природа волн Де Бройля из-за отказа от признания существования мирового эфира не объяснена в современной физике. Хотя очевидно, что это волновой процесс, неизбежно сопровождающий движение микрочастиц в окружающей их среде - мировом эфире. Тем не менее, известно, что длина волны Де Бройля определяет размеры электронных орбит атомов (вспомним, что Нильс Бор определил размеры орбит электронов в атоме водорода из условия целого количества укладывающихся на них волн Де Бройля), а, следовательно, размеры атомов и молекул, из которых состоят все материальные объекты окружающего нас мира. Сокращение длины волны Де Бройля в направлении движения согласно (22) вызывает сокращение длины любых материальных тел, состоящих из атомов и молекул, вдоль направления движения согласно (10), не зависящее от твёрдости образца и его химического состава.

ГИПОТЕЗА О ПРИРОДЕ МИРОВОГО ЭФИРА

Давайте будем пытаться высказывать и развивать гипотезу о природе мирового эфира, поскольку физики, находящиеся под контролем проповедников СТО, делать этого явно не собираются. Начнём с простого. Есть среда – мировой эфир. Есть так же положительно и отрицательно заряженные частицы. Одноимённо заряженные частицы отталкиваются друг от друга, разноимённо заряженные – притягиваются. Для меня лично не подлежит сомнению, что электростатические силы являются результатом разницы давлений, возникающих в среде - мировом эфире. Но каким образом одна и та же среда может на одноимённо заряженные частицы действовать отталкивающе, а на разноимённо – притягивающе? У меня не хватает воображения представить себе какой-нибудь иной механизм такого действия, кроме как считать, что отталкивание одноимённых зарядов и притягивание разноимённых является следствием некоего колебательного процесса, совершаемого положительно и отрицательно заряженными частицами в противофазе. Представим себе, что положительно и отрицательно заряженные частицы имеют в своём составе шарообразные ядра, которые совершают колебательные движения, то увеличивая, то уменьшая свой объём. Ядра у положительно и отрицательно заряженных частиц одинаковые, колеблются с одинаковой частотой и амплитудой, но, в противофазе. Когда ядро расширяется, оно создаёт вокруг себя давление выше среднего давления мирового эфира, когда ядро сжимается, вокруг заряженной частицы создаётся давление ниже среднего. Разница давлений в среде создаёт силы, отталкивающие одноимённые заряды, и притягивающие разноимённые. Но, чтобы такая схема работала, ядра всех заряженных частиц во всей Вселенной должны совершать колебательные движения абсолютно синхронно. То есть, в такой схеме понятие абсолютной одновременности классической физики имеет физическую, а не философскую основу. Количество совершённых колебаний описанного периодического процесса можно связать с течением времени. Это не само Время, но, во всяком случае, периодический процесс, лежащий в основе всех физических явлений, близкий к понятию «абсолютное Время Ньютона». Физический мир, таким образом, существует в рамках одного постоянно повторяющегося цикла времени, а ось времени от настоящего в прошлое и будущее представляет собой последовательность таких циклов.

СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ А. ЭЙНШТЕЙНА – ВЕЛИЧАЙШАЯ АФЕРА В ИСТОРИИ ФИЗИКИ

Благодаря факторам, крайне далёким от предмета и методов изучения явлений, применяемых в физической науке (типа Постановления ЦК ВКП(б) 1934 г. "По дискуссии о релятивизме", по которому за критику теории относительности отправляли в лагеря, постановления Президиума Академии Наук СССР от 1964 года о запрете публикации критики СТО в средствах массовой информации), КЛФП была безосновательно отвергнута и практически забыта. Вместо неё во все школьные и вузовские учебники физики была включена широчайше разрекламированная средствами массовой информации заведомо ложная и абсурдная “Специальная теория относительности” (СТО) А. Эйнштейна, что явило собой величайшую аферу в истории физики.

Ниже приводятся преобразования А. Эйнштейна (-1) – (-6) для некоторой системы K’, движущейся прямолинейно и равномерно относительно другой системы K, считающейся неподвижной, со скоростью V вдоль оси x. Чтобы отличать официальные формулы СТО от полученных из них производных формул и формул КЛФП будем помечать их знаком (-). Некоторые авторы абсолютно ложно называют уравнения Эйнштейна (-1) – (-6) уравнениями Эйнштейна-Лоренца или даже просто уравнениями Лоренца. Уравнения Эйнштейна (-1) – (-6) принципиально отличаются от уравнений Лоренца (13), (14) и по виду, и уже тем, что в них идёт речь не о размерах материальных тел, а о параметрах пространства и времени. То есть, входящие в уравнения Эйнштейна величины имеют иной физический смысл, чем в уравнениях Лоренца, хотя уравнение (-2) внешне похоже на (14). “Система координат”, рассматриваемая в СТО, сама по себе является объектом воображаемым. В СТО нигде не говорится, что в ней обязательно должен присутствовать материальный объект. По Эйнштейну получается, что если мы вообразили движение системы K’ относительно системы K в некоторой области пространства, даже если она не содержит ни каких материальных объектов, то параметры пространства и времени в этой области должны измениться. Таких чудес пока никто не наблюдал, но мы, всё-таки, продолжим рассмотрение СТО, поместив в движущуюся систему материальный объект, так же, как мы это делали при рассмотрении КЛФП, в надежде, что вместе с параметрами пространства в равной степени изменятся и его параметры. Итак, пусть оси обеих систем параллельны.

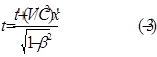
y=y’ (-5),

z=z’ (-6).

Это официальные формулы СТО. Их можно найти в [1] под номерами (63.15) и (63.16). В них правильнее было бы сразу внести некоторые изменения и дополнения. Дело в том, что фигурирующие в них величины t и t’ не имеют ни какого отношения к понятию “время”, используемому в классической физике, быту и преобразованиях Лоренца (13), (14). Эйнштейн назвал эти величины “пространство-время”. Это как бы время, но с пространственными составляющими, то есть текущее в разные стороны с разным темпом. В формулах (-1 … -4) вместо t и t’ правильнее было бы поставить tx и tx’. Кроме того, надо было бы добавить ty=ty’ и tz=tz’. Это очевидно, поскольку в формулах (-3) и (-4) t и t' зависят только от координаты x. Величина V в рассматриваемом случае, это проекция вектора скорости на координату x, то есть фактически это Vx. В то же время Vy=Vz=0. Подставляя эти значения в (-3) и (-4), получим ty=ty’, tz=tz’. Такой феномен, как время с пространственными составляющими пока в природе не обнаружен. Часы при повороте в пространстве относительно координаты x должны бы были менять скорость хода, если бы они измеряли “пространство-время” Эйнштейна. Не изобретён прибор эталон и единица для измерения пространства-времени. На этом обсуждение СТО, как абсурдной концепции, можно было бы и закончить. Но для людей с разным уровнем знаний, мышления, интеллекта различен и уровень убедительности доводов. Поэтому попытаемся показать, что время с пространственными составляющими является далеко не единственным абсурдом в СТО.

Обратим внимание на то, что преобразования Лоренца (13), (14), (как и преобразования Галилея (11), (12)) хотя и записаны в виде двух уравнений, но фактически это одно уравнение. Уравнения эквивалентны, поскольку преобразуются друг в друга перестановкой членов по разные стороны равенства по правилам эквивалентных преобразований математики. Из математической физики так же хорошо известно, что для описания прямолинейного и равномерного движения (в частности системы K’ относительно системы K) необходимым и достаточным является одно линейное уравнение, что имеет место в преобразованиях Галилея и Лоренца. Более того, известно, что каждому линейному (по времени) уравнению можно взаимно однозначно поставить в соответствие некую инерциальную систему, и всякое отличие в уравнениях приводит к отличиям в описываемых ими движущихся инерциальных системах. В СТО линейные уравнения (-1) и (-2) являются разными, поэтому они описывают не одну и ту же, а две разные системы K’ и K”, движущиеся относительно системы K. Анализ показывает, что системы K’ и K” движутся относительно K с одинаковой скоростью V (передние концы материальных объектов в этих системах), но всё равно это разные системы, поскольку в них имеются разные требования к длине материального объекта. В системе, описываемой уравнением (-1) для выполнения задаваемых им требований объект должен удлиняться, а в системе, описываемой уравнением (-2) – сокращаться относительно длины в состоянии покоя. Чтобы сделать это более наглядным перепишем уравнения (-1) и (-2) в виде (23) и (24) соответственно.

Оба уравнения (23) и (24) разбивают один и тот же физический отрезок x на две части, но в разной пропорции. Левые слагаемые в уравнениях (23) и (24) физически символизируют путь, пройденный началом координат систем K’ и K” или (в нашем случае) задним концом материальных объектов в этих системах, а правые – длину материального объекта, пересчитанную в масштаб длины неподвижной системы. Разница между длинами объекта в двух разных движущихся системах, описываемых уравнениями (-1) и (-2) составляет:

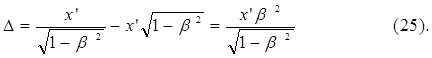D®¥ при V®C (или β→1).

То есть, при относительной скорости движения, стремящейся к скорости света, разница между длинами объектов в системах K’ и K” стремится к бесконечности. См. рис. 6

Vt x’q

D

K K’ K” V

Vt’/q x’/q

x

Рис.6

Для ещё большей наглядности рассмотрим числовой пример. Пусть C=300 ткм/1 (Тысяч километров в единицу “пространства-времени” Эйнштейна. Для измерения

“пространства-времени” Эйнштейна забыли придумать единицу измерения, а так же изобрести соответствующий измерительный прибор.); V=150 ткм/1; b=0.5; t=1; x’=100 ткм. Из (-3) находим t’=0.7. Тогда (23) примет вид 236.6=121.2+115.4, то есть, длина объекта должна со 100 ткм возрасти до 115.4 ткм. А (24) даёт другое разбиение 236.6=150+86.6. То есть, для выполнения условий, заданных этим уравнением объект со 100 ткм должен сократиться до 86.6 ткм. Но реальный материальный объект может быть либо растянут, либо сжат, сделать же то и другое для одного объекта одновременно невозможно. Значит уравнения (-1) и (-2) при длине материального объекта x’¹0, содержат противоречивые взаимно исключающие условия, не реализуемые для реальных физических объектов. Следовательно, теория, построенная на использовании уравнений (-1), (-2) является заведомо ложной. Некто может возразить, что в КЛФП тоже фигурирует два разных значения длины физического объекта. Но там это одна и та же физическая длина, измеренная двумя эталонами разного масштаба. В этом нет ничего необычного. Мы с подобным постоянно сталкиваемся в быту, измеряя длину разными линейками, изготовленными с невысокой точностью. В СТО же для удовлетворения условиям уравнений (-1) и (-2) длина одного и того же объекта, измеренная одним и тем же эталоном, должна иметь разные значения, и разница при V→C должна стремиться к бесконечности. Для реальных материальных объектов это физически не реализуемо. Можно посмотреть на ситуацию, рисуемую СТО, и по-другому, что уравнения (-1) и (-2) описывают две разные системы K’ и K”, движущиеся относительно K с одинаковой скоростью V. В них имеются одинаковые объекты, но для удовлетворения уравнениям А. Эйнштейна в одной из систем объект должен растянуться, а в другой сжаться. Это противоречит основополагающему принципу, благодаря которому физика вообще существует, как наука: представлению о том, что в одинаковых условиях одинаковые физические процессы протекают одинаково. Уравнения (-1) и (-2) противоречат этому фундаментальному принципу.

Официально (административным путём) в СТО утверждена только формула для сокращения длины объекта (аферисты, проповедующие СТО, подгоняют внешний вид формулы под сокращение Фиджеральда.) В [1] официальную формулу СТО для длины объекта можно найти под номером 64.1: