Статья: Технические задачи как средство развития профессионального мышления будущих инженеров

в

д г

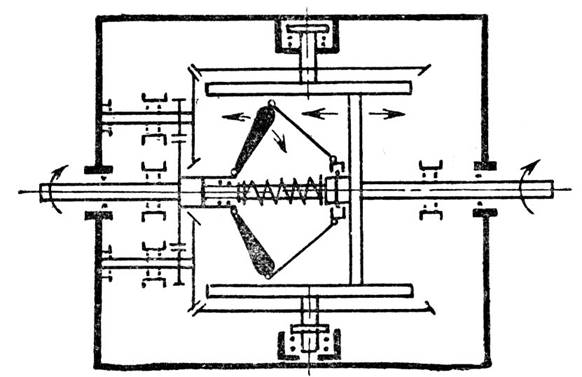
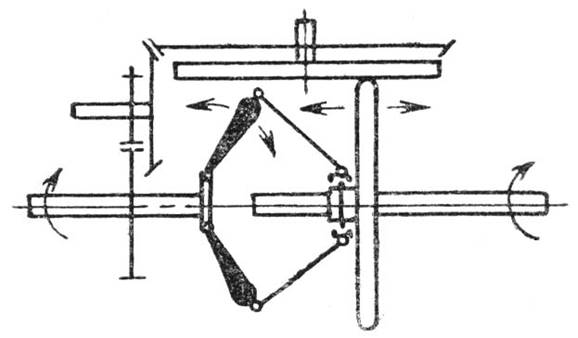
Рисунок 1. Схема саморегулируемой передачи.

Сформулируем задачу (постановка задачи) : задача на построение. Нужны две подсистемы: одна передает вращение, другая управляет числом оборотов, вернее – передаточным отношением. В этом примере изменяемыми характеристиками являются число оборотов ведущего вала и габариты объекта, неизменяемыми – число оборотов ведомого вала, соосность валов. Условная схема объекта показана на рис.1а.

Конкретизация условий, построение модели задачи:

- подсистема передачи вращения должна быть легкоуправляемой;

- на входе и выходе должна быть механическая энергия вращения;

- преобразование числа оборотов производится по программе.

Для механической передачи с учетом указанных условий можно найти легкоуправляемый вариант, например, фрикционная (лобовая) передача (модель задачи для подсистемы передачи вращения – см. рис.1б ).

Выявляем конфликтующую пару характеристик подсистемы передачи вращения объекта анализируем модель задачи (формулируем ТП₁ ) : ведомый и ведущий валы должны быть сосны, а в предложенной модели задачи этой подсистемы они не соосны (ТП). Формулируем ФП₁ : валы должны быть сосны и валы не должны быть соосны.

Нахождение принципиального решения технической задачи для первой подсистемы .

Формулировка идеального конечногорезультата для первой подсистемы: валы сами должны устранить вредноесвойство – несоосность.

Разрешение ФП₁ ТП₁ первой подсистемы : можно ввести преобразование в пространстве – зубчатую передачу, а чтобы она не мешала, сместить одно зубчатое колесо на край, а другое объединить с ведущим фрикционом (рис.1в).

Сформулируем модель задачи для подсистемы управления передаточным отношением: использовать энергопоток уже имеющий необходимую пространственно-временную организацию, а именно – ведущий (входной) вал. На него надо навесить центробежный регулятор и двигать с его помощью ведомый фрикционный диск ( рис. 1г ).

Выявляем конфликтующую пару второй подсистемы, анализируем модель задачи (формулируем ТП₂ ): центробежный регулятор – фрикционная передача, т. к. программу перемещения ведомого фрикционного колеса при изменении оборотов ведущего вала трудно реализовать: центробежная сила пропорциональна квадрату числа оборотов, а перемещение фрикционного колеса должно быть пропорционально первой степени. Формулируем ФП₂ :центробежная сила должна быть пропорциональна квадрату числа оборотов вала и не должна бытьпропорциональна квадрату числа оборотов. Нахождение принципиального решения технической задачи для второй подсистемы.

Формулировка идеального конечного результата для второй подсистемы: центробежный регулятор и фрикционная передача должны сами устранять вредное свойство.

Разрешение ФП₂ и ТП₂ второй подсистемы :в данном случае можно использовать Стандарт № 3 – введением между двумя взаимодействующими объектами (центробежный регулятор с ведущим валом и ведомый вал) третьего объекта являющегося видоизменением одного из них: пружины переменной жесткости.

На основании изложенного становится ясным способ работы объекта и принципиальная схема его реализации (см. рис.1д).

Приведенный выше пример решения технической задачи наглядно демонстрирует применение алгоритма и некоторых стандартных решений. Однако такие задачи целесообразно предлагать студентам уже имеющим некоторый опыт применения алгоритма и стандартов решения технических задач, т.е. в конце первого и на втором году обучения физике.

Применяемый алгоритм показывает путь решения технической задачи, но не уменьшает трудоемкости ее решения. При выполнении действий по устранению физического противоречия студентам приходится самостоятельно знакомится с большим объемом литературы для выявления физических эффектов и явлений, на основе которых можно строить решение задачи. Первокурсникам, которые только начинают изучать физику и находятся в начале процесса развития навыков решения технических задач, мы предлагаем в помощь, разработанную нами компьютерную программу

«Физический эффект». Названная программа представляет собой совокупность клиентского приложения и базы данных. Клиентское приложение предоставляет пользовательский интерфейс для управлениями двумя списками: списком физических эффектов и списком физических параметров. Приложение предоставляет средства для определения по заданному набору физических параметров конечного множества физических эффектов, которые оказывают влияние на значения этих параметров. Также можно определить конечное множество физических параметров, характеризующих тот или иной физический эффект.

Приведем пример решения технической задачи с помощью программы «Физический эффект».

Задача. Необходимо определить момент начала закипания смеси жидкостей, находящейся в не прозрачном герметичном реакторе. Пар над смесью жидкостей имеет постоянно изменяющееся давление, температуру и концентрацию веществ. Теоретический расчет, как и визуальное наблюдение невозможны.

Постановка задачи.

1. Цель: поиск физического эффекта, позволяющего определить начало закипания смеси жидкостей.

2. Ограничения: 1. Визуальное наблюдение исключено. 2. Непрерывное изменение режима исключает возможность определения начала закипания по величине температуры, давлению или концентрации вещества.

3. Изучим, особенности начала кипения, воспользовавшись описанием явления в программе «Физ. эффект». Одним из признаков начала закипания жидкости является возникновение на гладкой и спокойной поверхности неровностей и бугров при всплывании и разрыве пузырьков пара над поверхностью жидкости в момент начала кипения. Кроме того, возникает характерный шум при бурлении жидкости.

4. Изменяемые параметры: изменение формы поверхности (бурление),