Учебное пособие: Фінансовий ринок та ризик

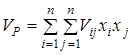, (3.1)

за умови, що забезпечується задане значення очікуваної ефективності портфеля :

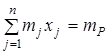, (3.2)

і виконується бюджетний баланс:

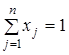. (3.3)

При комбінуванні в портфелі двох видів ризикових цінних паперів з характеристиками прибутковості і ризику , тобто й і коефіцієнтом кореляції модель Марковица має вид :

, (3.4)

.

Модель ефективного портфеля з без ризиковим компонентом (задача Тобина).

Ця задача відрізняється від моделі (3.1)-(3.3) тим, що інвестор крім ризикових цінних паперів враховує також можливість безризикових вкладень з ефективністю в частках . Задача Тобина формулюється в такий спосіб: знайти частки , що минимизують ризик портфеля :

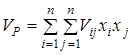, (3.5)

при обмеженнях:

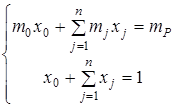(3.6)

З задачі Тобина випливає поняття цінного папера. Величина того цінного папера показує, яка частина ринкової прибутковості приходиться на прибутковість тої фірми:

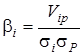, (3.7)

де - коваріація доходностей тої фірми і ринкового портфеля;

- ризик того цінного папера і ринкового портфеля.

Тоді прибутковість того цінного папера, що входить у портфель, визначається по формулі :

(3.8)

Якщо , то це значить, що прибутковість того цінного папера більше ринкової; при - її прибутковість дорівнює ринкової; при - прибутковість цінного папера менше ринкової, але більше, ніж безризиковий відсоток .

Ринкова ціна ризику визначається у виді:

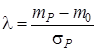, (3.9)

де - прибутковості портфеля цінних паперів і безризикова прибутковість;

- ризик портфеля.

Задача.

Знайти оптимальний портфель на траєкторії ефективних комбінацій із двох ризикових цінних паперів з характеристиками

, ; , , , .

Вказівки для рішення задачі

1. Записати рівняння ризику портфеля, скориставшись формулою (3.4).

2. Виключити , записати рівняння ефективної траєкторії.

3. Знайти абсцису крапки дотику на границі ефективності, записавши рівняння дотичної до функції в крапці дотику :

.