Учебное пособие: Физика
![]() .
.
Интегрируя выражение (1.5) в интервале времени от t0 до t , получим формулу, позволяющую вычислить путь, пройденный телом за время t -t0 если известна зависимость от времени его скорости v (t )
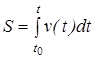 . (1.6)
. (1.6)
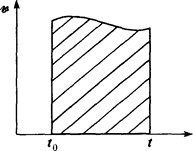
Геометрический смысл этой формулы ясен из рисунка. По определению интеграла пройденный путь представляет собой площадь, ограниченную кривой v =v (t ) в интервале от t0 до t .В случае равномерного движения, когда скорость сохраняет свое постоянное значение во все время движения, v =const ; отсюда следует выражение
![]() , (1.7)
, (1.7)
где S0 ‑ путь, пройденный к начальному времени t0 .
Производную скорости по времени, которая является второй производной по времени от радиус-вектора, называют ускорением точки:
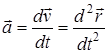 . (1.8)
. (1.8)
Вектор ускорения а направлен вдоль вектора приращения скорости dv . Пусть а = const . Этот важный и часто встречаемый случай носит название равноускоренного или равнозамедленного (в зависимости от знака величины а) движения. Проинтегрируем выражение (1.8) в пределах от t = 0 до t :
![]() (1.9)
(1.9)
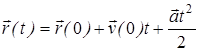 (1.10)
(1.10)
и используем следующие начальные условия: ![]() .
.
Таким образом, при равноускоренном движении
![]()
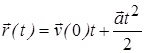 . (1.11)
. (1.11)
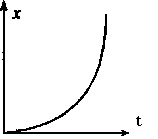
В частности, при одномерном движении, например вдоль оси X , 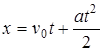 . Случай прямолинейного движения изображен на рис. При больших временах зависимость координаты от времени представляет собой параболу.
. Случай прямолинейного движения изображен на рис. При больших временах зависимость координаты от времени представляет собой параболу.
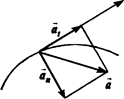
В общем случае движение точки может быть криволинейным. Рассмотрим этот тип движения. Если траектория точки произвольная кривая, то скорость и ускорение точки при ее движении по этой кривой меняются по величине и направлению.
Выберем произвольную точку на траектории. Как всякий вектор, вектор ускорения можно представить в виде суммы его составляющих по двум взаимно перпендикулярным осям. В качестве одной из осей возьмем направление касательной в рассматриваемой точке траектории, тогда другой осью окажется направление нормали к кривой в этой же точке. Составляющая ускорения, направленная по касательной к траектории, носит название тангенциального ускорения at , а направленная ей перпендикулярно — нормального ускорения an .
Получим формулы, выражающие величины at , и an через характеристики движения. Для простоты рассмотрим вместо произвольной криволинейной траектории плоскую кривую. Окончательные формулы остаются справедливыми и в общем случае неплоской траектории.
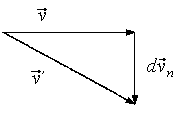

Благодаря ускорению скорость точки приобретает за время dt малое изменение dv . При этом тангенциальное ускорение, направленное по касательной к траектории, зависит только от величины скорости, но не от ее направления. Это изменение величины скорости равно dv . Поэтому тангенциальное ускорение может быть записано как производная по времени от величины скорости:
![]() . (1.12)
. (1.12)
С другой стороны, изменение dvn , направленное перпендикулярно к v , характеризует только изменение направления вектора скорости, но не его величины. На рис. показано изменение вектора скорости, вызванное действием нормального ускорения. Как видно из рис. ![]() , и, таким образом, с точностью до величины второго порядка малости величина скорости остается неизменной v =v' .
, и, таким образом, с точностью до величины второго порядка малости величина скорости остается неизменной v =v' .
Найдем величину an . Проще всего это сделать, взяв наиболее простой случай криволинейного движения — равномерное движение по окружности. При этом at =0. Рассмотрим перемещение точки за время dt по дуге dS окружности радиуса R .

Скорости v и v' , как отмечалось, остаются равными по величине. Изображенные на рис. треугольники оказываются, таким образом, подобными (как равнобедренные с равными углами при вершинах). Из подобия треугольников следует ![]() , откуда находим выражение для нормального ускорения:
, откуда находим выражение для нормального ускорения:
 . (1.13)
. (1.13)