Учебное пособие: Кінематика поступального руху
Величина
(1.3)
Називається середньою швидкістю руху за час 
. Напрямок середньої швидкості співпадає з напрямком 
. Якщо в (1.3) перейти до границі при →0, то отримаємо вираз для миттєвої швидкості 
:
Вектор швидкості напрямлений по дотичній до траєкторії в сторону руху (рис. 3).
По мірі зменшення шлях ∆ s все дужче буде приближатися до 
, тому
Тобто 
. Якщо вираз ds = υdt проінтегрувати по часу в межах від t до t +∆ t , то і довжину шляху, пройденого точкою за:
.
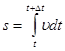Шлях, пройдений точкою за проміжок часу від t 1 до t 2 , дається інтегралом:
.
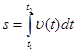2.4 Прискорення
В разі нерівномірного руху важливо те, як змінюється швидкість з плином часу. Фізичну величину, яка характеризує бистроту зміни швидкості по модулю і напрямку, називають прискоренням .
Нехай вектор задає швидкість точки в момент часу t. За час рухома точка перейшла в положенні В набула швидкість, відмінну від як по модулю, так і за напрямком, рівну +
. Перенесемо вектор 
в точку В і знайдемо 
(рис. 4).
Середнім прискоренням нерівномірного руху в інтервалі від t до t +∆ t є:
,
що називається миттєвим прискоренням 
.
Прискорення - це векторна величина, рівна похідній швидкості по часу:
.
Розкладемо вектор на дві складові. Для цього з точки А (рис. 4) за напрямком швидкості відкладемо вектор AD, по модулю дорівнює . Очевидно, що вектор CD, рівний 
, являє собою зміну швидкості по модулю за час : 
. Друга складова вектора 
характеризує зміну швидкості за час ∆ t по напрямку. Тангенціальна складова прискорення
:
.
Визначимо другу складову прискорення. Припустимо, що точка В достатньо близька до точки А, тому ∆ s можна вважати дугою кола з деяким радіусом r , який мало відрізняється від хорди АВ. Тоді з подібності трикутників AOB і EAD слідує 
, але так, як AB =υ∆ t , тому 
. При ∆ t
, томукут EADнаближається до нуля, а так, як трикутник EADрівнобедрений, то кут ADEміж 
та наближається до прямого. При 
вектори та виявляються взаємно перпендикулярними. Вектор швидкості напрямлений по дотичній до траєкторії, тому вектор , перпендикулярний швидкості, буде напрямлений до центра кола її кривизни. Друга складова прискорення дорівнює:
і називається нормальною складовою прискорення і напрямлена по нормалі до траєкторії до центра її кривизни.
Повне прискорення тіла геометричною сумою тангенціальної та нормальної складових:
.
З урахуванням тангенціальної і нормальної складових прискорення рух можна класифікувати наступним чином:
1) 
- прямолінійний рівномірний рух;
2) 
- прямолінійний рівнозмінний рух; при такому виді руху