Учебное пособие: Математические и логические основы информатики

Наконец, доказательство теоремы вида A~B можно заменять доказательством равносильной ей противоположной теоремы ØА~ØВ. (В равносильности этих теорем легко убедиться с помощью таблиц истинности.)

Изложив основные структуры математических доказательств, мы надеемся, что читатель теперь по иному будет относиться к доказательству любой теоремы из курсов линейной алгебры, аналитической геометрии, математического анализа и т.д. Приступая к изучению доказательства любой теоремы, прежде всего, необходимо выяснить структуру доказательства, постараться отнести его к одному из рассмотренных четырех видов, а уже затем изучать само доказательство, четко представляя ту идею, которую применил автор теоремы для того, чтобы ее доказать.

Применение логики высказываний к анализу и синтезу

переключательных (контактных) схем

Переключательной (или контактной ) схемой мы будем называть участок электрической цепи, включающий ряд переключателей (контактных выключателей), подобный приведенному на рис.2.2.

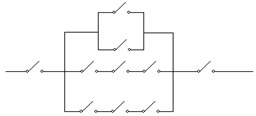
Рис.2.2. Вид переключательной схемы.

Каждому переключателю схемы сопоставим пропозициональную переменную Xi, которая будет принимать значение И (истина) или Л (ложь), если соответствующий переключатель замкнут или разомкнут (то есть, не проводит электрический ток).

Поскольку функция участка электрической цепи состоит в том, чтобы проводить электрический ток, то два участка, содержащие одни и те же переключатели и проводящие или не проводящие ток при одном и том же состоянии всех выключателей , мы будем считать "равными" и не различать между собой.

Легко сообразить, что участку цепи, представляющему собой последовательное соединение двух переключателей X1 и X2 будет отвечать формула логики высказываний, представляющая собой конъюнкцию пропозициональных переменных X1 и X2, то есть, X1&X2 (что означает, что такой участок проводит ток тогда и тогда, когда оба переключателя X1 и X2 замкнуты), а участку цепи, представляющему собой параллельное соединение двух переключателей X1 и X2 - формула, представляющая собой дизъюнкцию пропозициональных переменных X1 и X2, то есть, X1ÚX2. Сказанное представлено на рис. 2.3.

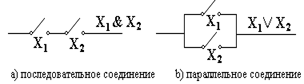
Рис. 2.3. Соответствие формул логики высказываний видам соединения переключателей.

Условимся обозначать через И всегда замкнутый контакт, а через Л - всегда разомкнутый. На схемах это будет выглядеть так, как представлено на рис. 2.4.

Рис.2.4. Соответствие логических констант всегда замкнутому и всегда разомкнутому контактам.

Условимся, наконец, обозначать через Xi и ØXi такую пару контактов, что когда контакт Xi замкнут, контакт ØXi обязательно разомкнут, и наоборот. Техническое осуществление такой пары контактов показано на рис.2.5.

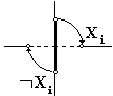
Рис.2.5. Реализация контактов Xi и ØXi.

Ясно, что параллельное и последовательное соединение переключательных схем обладает свойствами коммутативности, ассоциативности, идемпотентности.

Несколько сложнее проверяется выполнимость двух законов дистрибутивности:

Приведены попарно эквивалентные переключательные схемы, подтверждающие справедливость указанных законов дистрибутивности для переключательных схем.

Таким образом, все законы логики высказываний имеют аналоги в логике переключательных схем. Это, во-первых, позволяет моделировать сложные высказывания с помощью электрических цепей. Во-вторых, конструировать (синтезировать) переключательные схемы, удовлетворяющие наперед заданным условиям (которые могут быть и достаточно сложными).

Булевские функции

Многим из читателей, мы полагаем, приходилось иметь дело с так называемыми числовыми функциями: алгебраическими, тригонометрическими, логарифмическими и т.д. Все они характеризовались тем, что область определения и область значений функций представляли собой подмножества множества действительных чисел.

Например, функция y = f(x), задаваемая формулой y = sin(x) + 1, имеет в качестве области определения (обычно обозначается буквой Х) все множество действительных чисел, а в качестве области значений (чаще обозначаемой буквой Y) множество неотрицательных чисел, принадлежащих интервалу [0, 2]; функция y = j(x) , задаваемая формулой j(x)=|lgx|+5, в качестве области определения имеет множество всех положительных действительных чисел, а в качестве области значений - множество положительных действительных чисел, больших 5.

Рассматриваемые нами здесь булевские (логические ) функции характеризуются тем, что аргументы и сама функция принимают значения из множества логических констант {И, Л}.

В теории булевских функций чаще используются "числовые" эквиваленты логических констант: 1 вместо И, 0 - вместо Л. Ниже мы будем придерживаться именно этих обозначений.

Булевская функция в общем случае может содержать n аргументов: y=f(x1,x2,…,xn).

Как и математические функции, булевские функции могут задаваться: словесно, таблично или аналитически. Мы будем использовать последние два способа задания булевских функций: табличный (в виде таблиц истинности) и аналитический (в виде формул логики высказываний). Одна и та же функция может, естественно, задаваться по-разному.

Булевские функции одной переменной

Булевских функций от одной переменной всего 4. Эти функции и задающие их формулы логики высказываний приведены в следующей таблице:

x	0	1	Формулы логики высказываний, задающие функции
φ1	0	0	φ1(x) = 0 (константа 0)
φ2	0	1	φ2(x) = x (совпадает с переменной х)
φ3	1	0	φ3(x) = Øx (является отрицанием переменной х)
φ4	1	1	φ4(x) = 1 (константа 1)

Булевских функций от двух переменных всего насчитывается 16. Все они представлены в следующей таблице:

x	0	0	1	1	Формулы логики высказываний, задающие функции
y	0	1	0	1
f1	0	0	0	0	f1(x,y) = 0 (константа 0)
f2	0	0	0	1	f2(x,y) = x&y (конъюнкция)
f3	0	0	1	0	f3(x,y) = Ø(xÉy) (отрицание импликации)
f4	0	0	1	1	f4(x,y) = x (совпадает с переменной x)
f5	0	1	0	0	f5(x,y) = Ø(yÉx) (отрицание обратной импликации)
f6	0	1	0	1	f6(x,y) = y (совпадает с переменной y)
f7	0	1	1	0	f7(x,y) = xÅy (строгая дизъюнкция)
f8	0	1	1	1	f8(x,y) = xÚy (дизъюнкция)
f9	1	0	0	0	f9(x,y) = Øx&Øy (конъюнкция отрицаний)
f10	1	0	0	1	f10(x,y) = x~y (эквиваленция)
f11	1	0	1	0	f11(x,y) = Øy (отрицание y)
f12	1	0	1	1	f12(x,y) = yÉx (обратная импликация)
f13	1	1	0	0	f13(x,y) = Øx (отрицание x)
f14	1	1	0	1	f14(x,y) = xÉy (импликация)
f15	1	1	1	0	f15(x,y) = Ø(x&y) (отрицание конъюнкции)
f16	1	1	1	1	f16(x,y) = 1 (константа 1)