Учебное пособие: Методы исследования операций
при условиях
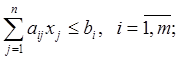(6)
. (7)
Двойственная задача
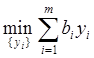(8)
при условиях
(9)
. (10)
Сопоставляя формы записи прямой и двойственной задач, можно установить между ними следующие взаимосвязи:
1) если прямая задача является задачей максимизации, то двойственная будет задачей минимизации, и наоборот;
2) коэффициенты целевой функции прямой задачи c1, c2, …, cn становятся свободными членами ограничений двойственной задачи;
3) свободные члены ограничений прямой задачи b1, b2, …, bm становятся коэффициентами целевой функции двойственной задачи;
4) матрицу ограничений двойственной задачи получают транспонированием матрицы ограничений прямой задачи;
5) если знаки всех неравенств в ограничениях прямой «£», то в двойственной задаче все ограничения будут иметь знак «³»;
6) число ограничений прямой задачи равно числу переменных двойственной задачи, а число ограничений двойственной задачи равно числу переменных прямой задачи.
Переменные y1, y2,…, ym двойственной задачи иногда называют «теневыми ценами».
Двойственную задачу выгоднее решать, чем исходную прямую, если в прямой задаче при малом количестве переменных имеется большое количество ограничений (т > n).
Связь между оптимальными решениями прямой и двойственной задач устанавливают посредством следующих теорем теории двойственности.
Теорема. Если x0 и у0 — допустимые решения прямой и двойственной задач, т. е. если Ах0 £ b и АTy0 ³ с, то
cTx0£ bTy0,
т. е. значения целевой функции прямой задачи никогда не превышают значений целевой функции двойственной задачи.
Теорема(основная теорема двойственности). Если x0 и у0 — допустимые решения прямой и двойственной задач и если cTx0=bTy0, то x0 и у0 — оптимальные решения пары двойственных задач.
Теорема. Если в оптимальном решении прямой задачи i-е ограничение выполняется как строгое неравенство, то оптимальное значение соответствующей двойственной переменной равно нулю.
Смысл этой теоремы состоит в следующем. Если некоторый ресурс bi имеется в избытке и i-е ограничение при оптимальном решении выполняется как строгое неравенство, то оно становится несущественным, и оптимальная цена соответствующего ресурса равна 0.
Теорема. Если в оптимальном решении двойственной задачи ограничение j выполняется как строгое неравенство, то оптимальное значение соответствующей переменной прямой задачи должно быть равно нулю.
Экономическая интерпретация этой теоремы: поскольку величины yj представляют собой цены соответствующих ресурсов, то 
— это затраты на i-й технологический процесс, величина сi — прибыль от реализации на единицу изделия. Поэтому с экономической точки зрения теорема означает следующее: если i-й технологический процесс оказывается строго невыгодным с точки зрения оптимальных цен ресурсов уопт, то в оптимальном решении прямой задачи интенсивность использования данного технологического процесса хi должна быть равна 0.
Таким образом, теорема выражает принцип рентабельности оптимального организованного производства.
Теорема (теорема существования). Прямая и двойственная задачи имеют оптимальные решения тогда и только тогда, когда обе они имеют допустимые решения.
Теорема (теорема двойственности). Допустимый вектор x0 оптимален тогда и только тогда, когда в двойственной задаче имеется такое допустимое решение уо, что