Учебное пособие: Основные понятия и образы квантовой механики

1.3.4. Сформулируем условие самосопряженности операторов. Выделим из операторных уравнений (1.1) и (1.4) собственные значения и , не нарушая равенств. Учтем, что символ оператора означает преобразование функции, записанной справа от него.* Поэтому, чтобы не нарушить смысла преобразования, влекущего за собой нарушение равенств (1.1) и (1.4), домножим слева первое из них на , а второе на. Затем следует справа домножить каждую из частей (правую и левую) обоих уравнений на произведение дифференциалов всех координат и результат проинтегрировать во всем пространстве изменения аргументов. Сравним ход этих преобразований:

, ;

, ;

, ;

, .

Вообще говоря, это дело вкуса и удобства. Важно далее всюду соблюдать оговоренные однажды правила математического синтаксиса.

Правые части этих последних равенств равны:

и

Поэтому равны и левые, т. е. получаем равенство (1.5), которое выражает условие самосопряженности операторов, имеющих действительные собственные значения.

(1.5)

1.3.5. В формуле (1.5) представлена функция и ее комплексно-сопряженный "двойник" , а в общем виде эрмитов оператор связывает две разные функции f и g аналогичной формулой:

(1.6)

Обратим внимание читателя на то, что процедура комплексного сопряжения оператора и перевод его в связана с тем, что мнимая единица в качестве численного параметра входит в конструкцию оператора.

1.3.6. Запись уравнений типа .(1,5) и (1.6) можно упростить и одновременно придать им дополнительный смысл, используя символы-скобки и , предложенные Дираком и называемые бра- и кет-символами соответственно (от англ. brасkets – скобки). Итак, вместо знаков интеграла, функций и дифференциалов переменных, образующих вместе операцию интегрирования, запишем эквивалентные символы:

и

где называется бра-вектором, а – кет-вектором. В таком случае интеграл от произведения двух функций приобретает вид скалярного произведения

(1.7)

Если в интеграл введем оператор, то получаем также символическое скалярное произведение

, (1.8)

в котором вектор преобразован оператором в новую волновую функцию-вектор, равный .

Таким образом, в этой записи очень многие важные интегралы квантовой механики оказываются просто скалярными произведениями различных бра- и кет-векторов. Формула (1.6) в бракет-символах приобретает вид:

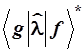= (1.9)

1.3.7. Из условия (1.6) или (1.9) вытекает чрезвычайно важное свойство собственных функций эрмитова оператора, называемое свойством ортогональности. Поясним смысл этого определения. Для этого рассмотрим две разные собственные функции эрмитова оператора, например, f и g, которым отвечают разные ненулевые собственные числа и соответственно, т.е. справедливы операторные равенства

и (1.10)

Образуем скалярные произведения

и (1.11)

Из первого скалярного произведения вычтем произведение, комплексно-сопряженное второму, и с учетом (1.11) получим:

(1.12)

По определению эрмитова оператора получаем: