Учебное пособие: Оцінка результату і похибки прямих вимірювань
Відповідно до критерію Фішера, який використовується при числі серій ![]() , різницю середніх арифметичних результатів серій спостережень вважають допустимою, якщо виконується умова
, різницю середніх арифметичних результатів серій спостережень вважають допустимою, якщо виконується умова
 , (4.2)
, (4.2)
де![]() - оцінка міжгрупової дисперсії;
- оцінка міжгрупової дисперсії;
![]() - середнє значення оцінок внутрішньогрупових дисперсій;
- середнє значення оцінок внутрішньогрупових дисперсій;
![]() - відсоткові значення розподілу Фішера. Їх знаходять залежно від числа степенів вільності
- відсоткові значення розподілу Фішера. Їх знаходять залежно від числа степенів вільності ![]() для різних рівнів значущості (найбільш широко використовуються 1% і 5%) за таблицями, які приведені у відповідній літературі [3,26]. Причому:
для різних рівнів значущості (найбільш широко використовуються 1% і 5%) за таблицями, які приведені у відповідній літературі [3,26]. Причому: ![]() - число степенів вільності чисельника
- число степенів вільності чисельника ![]() ;
; ![]() - число степенів вільності знаменника
- число степенів вільності знаменника ![]() , де
, де  - число спостережень у всіх Lсеріях;
- число спостережень у всіх Lсеріях; ![]() - число спостережень в j-й серії,
- число спостережень в j-й серії, ![]() .
.
Методика перевірки однорідності результатів ![]() серій спостережень за критерієм Фішера:
серій спостережень за критерієм Фішера:
1) обчислюють середнє арифметичне значення результатів кожної серії спостережень
 ,
, ![]() ;
;
2) обчислюють міжгрупове (загальне) середнє арифметичне значення для всього обсягу N результатів спостережень (в усіх серіях)
 (4.3)
(4.3)
Якщо всі серії складаються з однакового числа спостережень ![]() , то формула (4.3) спрощується
, то формула (4.3) спрощується
 ;
;
3) знаходять незміщену оцінку міжгрупової дисперсії результатів спостережень (розсіювання між груповими середніми арифметичними)
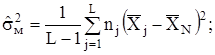
4) визначають середнє арифметичне значення незміщених оцінок внутрішньогрупових дисперсій результатів спостережень (середнє розсіювання всередині груп):
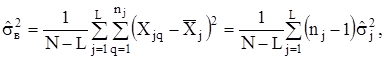 (4.4)
(4.4)
де 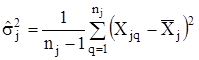 (4.5)
(4.5)
- незміщена оцінка внутрішньогрупової дисперсії результатів спостережень j-ї серії, ![]() ;
;
5) знаходять значення ![]() за таблицею Фішера і перевіряють виконання нерівності (4.2), тобто критерію Фішера. Якщо значення відношення
за таблицею Фішера і перевіряють виконання нерівності (4.2), тобто критерію Фішера. Якщо значення відношення ![]() знаходиться поза інтервалом, який визначається нерівністю (4.2), то це означає, що середні арифметичні результатів спостережень серій мають недопустимі зміщення. У такому разі приймають рішення про неоднорідність серій спостережень, тобто про неприпустимість різниці між їхніми середніми арифметичними значеннями. Для усунення цього ефекту необхідно знайти причину розходження між середніми арифметичними значеннями
знаходиться поза інтервалом, який визначається нерівністю (4.2), то це означає, що середні арифметичні результатів спостережень серій мають недопустимі зміщення. У такому разі приймають рішення про неоднорідність серій спостережень, тобто про неприпустимість різниці між їхніми середніми арифметичними значеннями. Для усунення цього ефекту необхідно знайти причину розходження між середніми арифметичними значеннями ![]() і в експериментальні дані відповідної серії (серій) внести додаткову поправку (поправки). Інколи, з метою виявлення за допомогою такої перевірки прогресуючого впливу будь-якого чинника, увесь масив експериментальних даних штучно розбивають на дві або більше серій.
і в експериментальні дані відповідної серії (серій) внести додаткову поправку (поправки). Інколи, з метою виявлення за допомогою такої перевірки прогресуючого впливу будь-якого чинника, увесь масив експериментальних даних штучно розбивають на дві або більше серій.
Для перевірки однорідності двох серій вимірювань, розподіл яких відрізняється від нормального, доцільно використовувати рангові критерії Уілкоксона і Сіджела-Тьюкі [25].
Критерії рівноточності результатів серій спостережень
Поряд з термінами “рівноточні” і “нерівноточні” результати спостережень (вимірювань) використовують також терміни “рівнорозсіяні” і “нерівнорозсіяні” результати спостережень, оскільки вони ґрунтуються на порівнянні і допустимості відмінностей оцінок внутрішньогрупових дисперсій (або СКВ) результатів спостережень. Для перевірки такої допустимості відмінностей використовують критерій Р. Фішера (при числі серій ![]() ) або критерій М. Бартлетта (при числі серій
) або критерій М. Бартлетта (при числі серій ![]() ).
).
Відповідно до критерію Фішера відмінність між незміщеними оцінками дисперсій ![]() результатів двох серій з числом спостережень
результатів двох серій з числом спостережень ![]() вважається допустимою, якщо виконується умова
вважається допустимою, якщо виконується умова
 . (4.6)
. (4.6)
Значення ![]() залежно від числа степенів вільності для рівнів значущості
залежно від числа степенів вільності для рівнів значущості ![]() наводяться в таблицях Фішера. Число степенів вільності для оцінки дисперсії
наводяться в таблицях Фішера. Число степенів вільності для оцінки дисперсії ![]() дорівнює
дорівнює ![]() , для оцінки дисперсії
, для оцінки дисперсії ![]() воно дорівнює
воно дорівнює ![]() . Оцінки дисперсій
. Оцінки дисперсій ![]() обчислюють за формулою (4.5), після цього перевіряють нерівність (4.6).
обчислюють за формулою (4.5), після цього перевіряють нерівність (4.6).
Критерій М. Бартлетта справедливий для ![]() і
і ![]() . Він ґрунтується на обчисленні
. Він ґрунтується на обчисленні ![]() - розподілу
- розподілу
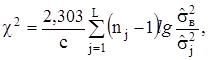 (4.7)
(4.7)
де  . (4.8)
. (4.8)
Оцінки дисперсій ![]() і
і ![]() обчислюють за формулами (4.4) і (4.5). Якщо в усіх серіях число спостережень
обчислюють за формулами (4.4) і (4.5). Якщо в усіх серіях число спостережень ![]() , то можна вважати c = 1.
, то можна вважати c = 1.
Критерій Бартлетта визначається нерівністю