Учебное пособие: Практикум по решению линейных задач математического программирования

Если величины и рассматривать как координаты точки плоскости, то совокупность точек плоскости, координаты которых удовлетворяют неравенству (1), называется областью решений данного неравенства. Следовательно, областью решений неравенства (1) является полуплоскость с граничной прямой линией .

Пример 1. Найти полуплоскость, определяемую неравенством

.

Решение. Строим прямую по двум точкам, например, по точкам пересечения с осями координат (0; 4) и (6; 0). Эта линия делит плоскость на две части, т.е. на две полуплоскости. Берем любую точку плоскости, не лежащую на построенной прямой. Если координаты точки удовлетворяют заданному неравенству, то областью решений является та полуплоскость, в которой находится эта точка. Если же получаем неверное числовое неравенство, то областью решений является та полуплоскость, которой эта точка не принадлежит. Обычно для контроля берут точку (0; 0).

Подставим и в заданное неравенство. Получим . Следовательно, полуплоскость «к нулю» является областью решений данного неравенства (заштрихованная часть рис. 1).

Пример 2. Найти полуплоскость, определяемую неравенством

.

Решение. Строим прямую , например, по точкам (0; 0) и (1; 3). Т.к. прямая проходит через начало координат, точку (0; 0), то нельзя брать ее для контроля. Возьмем, например, точку (– 2; 0) и подставим ее координаты в заданное неравенство. Получим . Это неверно. Значит, областью решений данного неравенства будет та полуплоскость, которой не принадлежит контрольная точка (заштрихованная часть рис. 2).

2. Область решений системы линейных неравенств.

Пример. Найти область решений системы неравенств:

Решение. Находим область решений I-го неравенства (рис. 1) и II-го неравенства (рис. 2).

Все точки части плоскости, где штриховка наложилась, будут удовлетворять и первому и второму неравенству. Таким образом, получена область решений заданной системы неравенств (рис. 3).

Если к заданной системе неравенств добавить условия и , то область решений системы неравенств 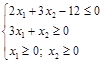будет находиться только в I координатной четверти (рис. 4).

Принцип нахождения решения системы линейных неравенств не зависит от количества неравенств, входящих в систему.

Примечание : Область допустимых решений (ОДР) если существует, то представляет собой замкнутый или незамкнутый выпуклый многоугольник.

3. Алгоритм графического метода решения ЗЛП

Если задача линейного программирования содержит только две переменные, то ее можно решить графическим методом, выполняя следующие операции:

1) Строим все полуплоскости, соответствующие ограничениям системы.

2) Находим область допустимых решений (ОДР), как множество точек, в котором пересекаются все построенные полуплоскости.

3) Строим вектор , выходящий из начала координат, где и – это коэффициенты при неизвестных в целевой функции . Этот вектор указывает направление возрастания целевой функции.

4) Перпендикулярно вектору проводим так называемую линию уровня (т.е. прямую , проходящую через начало координат).

5) Перемещаем линию уровня параллельно самой себе в направлении вектора (если задача на максимум (max )) или в противоположном направлении (если задача на минимум (min )) до тех пор, пока линия уровня имеет хотя бы одну общую точку с ОДР.

6) Находим координаты этой общей крайней точки, решая систему уравнений прямых, на пересечении которых она находится.

7) Подставляем эти координаты в целевую функцию и находим ее max (или min ).

Пример. Решить задачу линейного программирования графическим методом

max

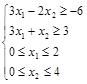
Решение. Третье и четвертое ограничения системы – двойные неравенства, преобразуем их к более привычному для подобных задач виду , это и , т.о. первое из полученных неравенств (или ) относится к условию неотрицательности, а второе к системе ограничений. Аналогично, это и .

Т.о. задача примет вид

max