Учебное пособие: Расчет и выбор аспирационного оборудования
где
(18)
(19)
(20)
Порядок расчета рассмотрим на примере.
1. На основании заданного гранулометрического состава строим интегральный график распределения частиц по крупности (воспользовавшись предварительно найденной интегральной суммой mi ) и находим медианный диаметр (рис. 3) dм = 3,4 мм > 3 мм, т.е. имеем случай перегрузки кускового материала и, следовательно, 
=0,03 м; Pу =7 Па (табл. 4). В соответствии с формулой (10) средний диаметр частиц 
.
2. По формуле (3) определяем площадь неплотностей нижнего укрытия (имея в виду, что L0 =1,5 м; b =0,6 м, при В =0,5 м (см. табл. 1)
Fн =2 (1,5 + 0,6) 0,03 = 0,126 м2
3. По формуле (2) определяем расход воздуха, поступающего через неплотности укрытия
Существуют другие формулы для определения коэффициента 
в т.ч. для потока мелких частиц, на скорости движения которых сказывается сопротивление воздуха [13, 14].
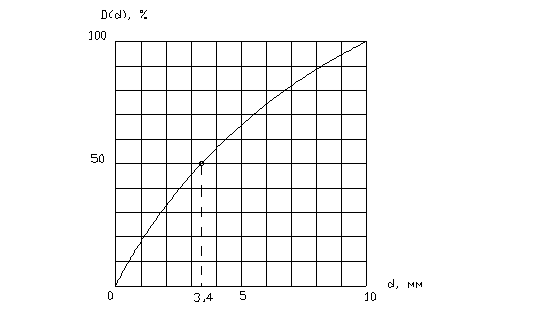
Рис. 3. Интегральный график распределения частиц по крупности
4. По формулам (5)… (7) находим скорости потока частиц в желобе:
м/с
м/с
м/с
следовательно
n = 4,43 / 5,87 =0,754.
5. По формуле (11) определяем сумму к.м.с. желоба с учетом сопротивления укрытий. При Fв =0,2 м2 по формуле (12) имеем
При h/H = 0,12/0,4 = 0,3, 
по табл. 5 находим ζn ep =6,5;
6. По формуле (14) находим объемную концентрацию частиц в желобе
7. По формуле (13) определяем коэффициент лобового сопротивления
частиц в желобе 
8. По формулам (8) и (9) находим соответственно число Бутакова–Нейкова и число Эйлера:
