Учебное пособие: Решение задач с помощью ЭВМ

Из определения алгоритма и рассмотренных примеров можно сформулировать следующие требования к его свойствам.

Такими свойствами являются:

· Дискретность (прерывность, раздельность) - алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.

· Определенность - каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.

· Результативность (конечность) - алгоритм должен приводить к решению задачи за конечное число шагов.

· Массовость - алгоритм решения задачи разрабатывается в общем виде, то есть, он должен быть применим для некоторого класса задач, различающихся только исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.

Средства, используемые для записи алгоритмов, в значительной степени определяются тем, для какого исполнителя предназначается алгоритм. Если алгоритм предназначен для исполнителя — человека, то его запись может быть не полностью формализована , на первое место здесь выдвигаются понятность и наглядность, поэтому для записи таких алгоритмов может использоваться естественный или графический язык, лишь бы запись отражала все основные особенности алгоритма. Для записи алгоритмов, предназначенных для исполнителей — автоматов, необходима формализация , поэтому в таких случаях применяют специальные формальные языки.

Словесная запись алгоритма . Словесная форма обычно используется для алгоритмов, ориентированных на исполнителя — человека. Команды алгоритма нумеруют, чтобы иметь возможность на них ссылаться. Приведем в качестве еще одного примера словесной формы записи алгоритма классический алгоритм Евклида для нахождения наибольшего общего делителя двух натуральных чисел:

Даны два целых положительных числа m и n. Требуется найти их наибольший общий делитель, т.е. наибольшее положительное число, на которое делится без остатка как m, так и n.

Суть алгоритма Евклида можно представить следующими тремя этапами.

1. Нахождение остатка. Разделим m на n. Пусть остаток равен г:

0<г< n.

2. Проверка остатка на равенство нулю. Если г = О, вычисление кончается, n — искомое число.

3. Замена m ← n, n ← г. Повторить этап 1.

Пример

1. Даны m = 125, n = 75. Наши наибольший общий делитель.

1) 125: 75 = 1. Частное равно 1, остаток от деления равен 50,

2) Остаток от деления не равен 0. Проводим замену переменных:

m = 75, n = 50 и повторяем процесс,

1) 75: 50= 1, m = 25.

2) m = 50, n = 25, г = 0.

Повторяем процедуру.

1) 50:25= 2.

2) Остаток от деления равен 0, поэтому n = 25 является наибольшим общим делителем.

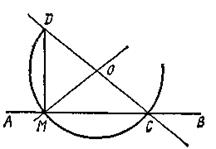
2. К отрезку АВ в точке М восстановить перпендикуляр. Алгоритм решения этой геометрической задачи может быть описан в виде четырех последовательных шагов (рис. 1).

1) Из произвольной точки О плоскости радиусом ОМ описать окружность, пересекающую отрезок АВ.

2) Отметить точку С пересечения окружности с отрезком АВ,

3) Найти точку D пересечения окружности с прямой ОС.