Учебное пособие: Синтез схемы шифратора и кодопреобразователя для управления 1-разрядным 7-сегментным индикатором
Логические элементы выполняют простейшие логические операции (конъюнкцию, дизъюнкцию, инверсию) над входной информацией, представленной в двоичной форме. Однако реализация произвольного вычислительного процесса, содержащего арифметические операции (сложение, вычитание, умножение) или логические процедуры (поиск, сортировка, сравнение, сдвиг и др.), также осуществляются схемами, состоящими из логических элементов. Таким образом, логические элементы образуют универсальную среду, обеспечивающую арифметическую и логическую обработку входной двоичной информации.
Работа с логическими элементами требует не только знакомства с их принципиальными схемами и техническими характеристиками, но и знания основных положений алгебры логики, теории переключательных схем, а также умения по определенным правилам синтезировать логические схемы с заданными характеристиками. Выполнение предлагаемого задания позволит приобрести основные необходимые для инженера навыки.
1. Порядок синтеза схемы шифратора и кодопреобразователя для управления 1-разрядным 7-сегментным индикатором
Проиллюстрируем методику решения задачи на примере.
1. Входные данные вводятся в унитарном коде. Унитарный код двоичного n-разрядного числа представляется 2n разрядами, только один из которых равен 1. Для преобразования этого кода в двоичный код следует применить шифратор. Шифратор должен иметь десять входов, каждому из которых соответствует одно из чисел 0, 1, 2,...,9. Число 9 в двоичном коде представляется разрядами: 1001, т.е. шифратор должен иметь четыре выхода. В соответствии с этими требованиями составляют таблицу истинности (табл.1).
Таблица 1
Таблица истинности шифратора
|
№ |
Входные переменные | Выходные переменные | ||||||||||||
| пп | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | y1 | y2 | y3 | y4 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 4 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
2. Получают логическую функцию шифратора в виде СДНФ путем записи “по единицам” (табл.1):
y1=x8+x9;
y2=x4+x5+x6+x7;
y3=x2+x3+x6+x7;
y4=x1+x3+x5+x7+x9
3. Используя полученные уравнения можно синтезировать функциональную схему шифратора в логическом базисе И, ИЛИ, НЕ (рис.1):
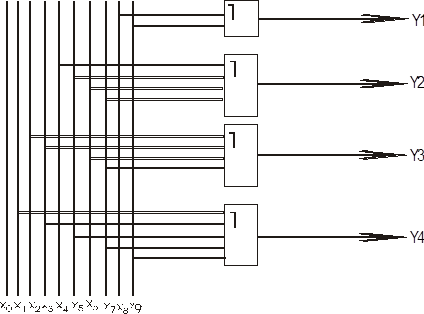
Рис.1. Функциональная схема шифратора на логических элементах или для синтеза шифратора в логических базисах И-НЕ или ИЛИ-НЕ следует применить закон двойной инверсии и закон инверсии (закон Де Моргана):
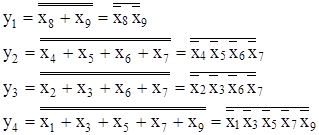
После выбора из табл.4 микросхем синтезируют принципиальную электрическую схему шифратора в заданном табл.5 базисе.
4. Допустим, что последние четыре цифры номера зачетной книжки образуют число 3011, т.е. должны индицироваться только стилизованные цифры 0, 1, 3, а при вводе остальных цифр - символ ![]()
5. При составлении таблицы истинности кодопреобразователя (табл.2) учитывают, что входные данные вводятся в двоичном коде, а наличие высокого потенциала на выходах кодопреобразователя y1, y2, y3,..., y7 вызывает свечение соответственно сегмента a, b, c, d, e, f, g 7-сегментного индикатора.
Таблица 2
Таблица истинности кодопреобразователя
| № | Входные | Выходные переменные | |||||||||
| пп | переменные | a | b | c | d | e | f | g | |||
| x4 | x3 | x2 | x1 | y1 | y2 | y3 | y4 | y5 | y6 | y7 | |
|
0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
|
1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 4 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 5 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 9 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 10. .15 | х | х | х | х | х | х | х | ||||
Символом “х” в табл. 2 обозначены безразличные состояния выходных переменных.
6. Для нахождения МДНФ применяют диаграммы Вейча-Карно (рис.2). Из табл.2 видно, что y1=y4; y2=y3; y5=y6.
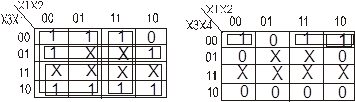
![]()
![]()