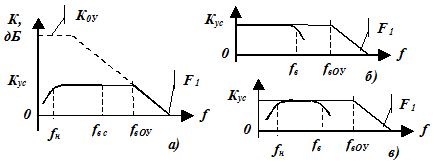Учебное пособие: Усилительные каскады на основе операционных усилителей
Используем во входной цепи инвертирующего усилителя конденсатор (рисунком 8.8,а ).
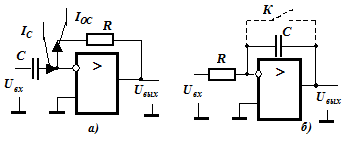
Рисунок 8.8. Дифференциатор и интегратор на основе ОУ
Известно, что ток, проходящий через емкость равен произведению емкости на производную от разности потенциалов на обкладках конденсатора. Учитывая (8.3), запишем
![]() (8.17)
(8.17)
где Iс – ток во входной цепи, проходящий через конденсатор С .
На основании (8.4) и (8.7), имеем
![]() ,
,
Или ![]() , (8.18)
, (8.18)
т.е. выходное напряжение является «проинвертированным» дифференциалом от входного, с коэффициентом пропорциональности, равным (R С ).
Поменяем местами конденсатор и резистор (рисунок 8.8,б). Тогда, произведя действия, аналогичные предыдущим, получим:
![]() ,
,
Интегрируя левую и правую части этого выражения по времени в пределах oт 0 до t , найдем
![]() , (8.19)
, (8.19)
где Uвых 0 – напряжение на выходе схемы при t = 0.
Таким образом, выходное напряжение пропорционально интегралу входного напряжения.
Так как Uвых 0 является и напряжением, до которого заряжен конденсатор в начальный момент времени, то это создает определенные сложности при практической реализации схем интеграторов – конденсатор подзаряжается постоянным входным током ОУ , что в конечном итоге приводит к режиму насыщения. Чтобы избежать этого явления, используют два метода борьбы:
периодического разряда емкости в результате замыкания ключа К , стоящего параллельно конденсатору;
обеспечению условий, при которых входной ток ОУ был бы значительно меньше токов, обусловленных сигналом.
2.5. Простейшие фильтры на основе ОУ
Сформируем входную цепь инвертирующего усилителя из последовательно соединенных конденсатора и резистора (рисунком 8.9,а).
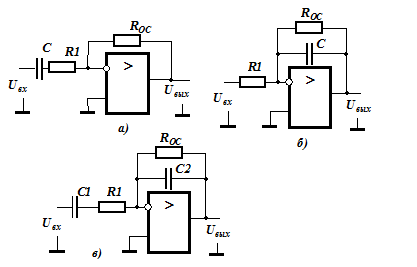
Рисунок 8.9. Простейшие фильтры на основе ОУ
Если повторить все математические преобразования, которые были проделаны для инвертирующего усилителя, то получим
![]() , (8.20)
, (8.20)
где ![]() .
.
Т.кю реактивное сопротивление емкости зависит от частоты сигнала f
![]() , (8.21)
, (8.21)
то модуль коэффициента усиления будет уменьшаться при уменьшении частоты. При f = 0 Кус = 0. При увеличении частоты он асимптотически будет приближаться к величине, соответствующей выражению (8.8). Таким образом, получено устройство, АЧХ которого соответствует фильтру верхних частот (ФВЧ , рисунок 8.10,а) первого порядка.